
如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B、C,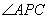 的平分线分别交AB、AC于点D、E.
的平分线分别交AB、AC于点D、E.
(1)证明: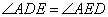 (2)若AC=AP,求
(2)若AC=AP,求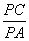 的值
的值

证明:(1)∵ PA是切线,AB是弦,∴ ∠BAP=∠C,又 ∵ ∠APD=∠CPE, ∴ ∠BAP+∠APD=∠C+∠CPE, ∵ ∠ADE=∠BAP+∠APD, ∠AED=∠C+∠CPE,∴ ∠ADE=∠AED.
(2)由(1)知∠BAP=∠C, 又∵ ∠APC=∠BPA,∴ △APC∽△BPA, ∴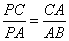 ,∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,∵ BC是圆O的直径,∴ ∠BAC=90°∴ ∠APC+∠C+∠BAP=180°-90°=90°,∴ ∠C=∠APC=∠BAP=
,∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,∵ BC是圆O的直径,∴ ∠BAC=90°∴ ∠APC+∠C+∠BAP=180°-90°=90°,∴ ∠C=∠APC=∠BAP=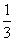 ×90°=30°.
×90°=30°.
在Rt△ABC中,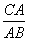 =
=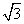 , ∴
, ∴ 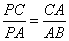 =
=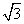


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
用n个不同的实数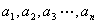 可得
可得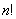 个不同的排列,每个排列为一行写成一个
个不同的排列,每个排列为一行写成一个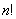 行的矩阵,对第
行的矩阵,对第 行
行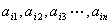 ,记
,记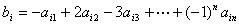 ,
,
(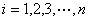 )例如由1、2、3排数阵知:由于此数阵中每一列各数之和都是12,所以
)例如由1、2、3排数阵知:由于此数阵中每一列各数之和都是12,所以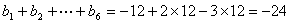 ,那么由1,2,3,4,5形成的数阵中,
,那么由1,2,3,4,5形成的数阵中,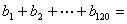 ( )
( )
A.—3600 B.1800 C.—1080 D.—720
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com