练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,

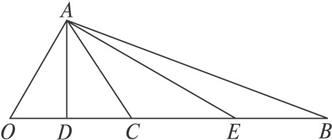
    试求：（1）△AOC为钝角三角形的概率；

    （2）△AOC为锐角三角形的概率.

    解：如图,由平面几何知识：

    当AD⊥OB时,OD=1；

    当OA⊥AE时,OE=4,BE=1.

    （1）当且仅当点C在线段OD或BE上时,△AOC为钝角三角形,

    记“△AOC为钝角三角形”为事件M,则P(M)==0.4,

    即△AOC为钝角三角形的概率为0.4.

    （2）当且仅当点C在线段DE上时,△AOC为锐角三角形,

    记“△AOC为锐角三角形”为事件N,则P(N)==0.6,

    即△AOC为锐角三角形的概率为0.6.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

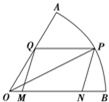    精英家教网如图，现在要在一块半径为1m．圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在AB弧上，点Q在OA上，点M，N在OB上，设∠BOP=θ．平行四边形MNPQ的面积为S．
    （1）求S关于θ的函数关系式；
    （2）求S的最大值及相应θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，AB是⊙O的切线，切点为A，OA=1，∠AOB=60°，则图中阴影部分的面积是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

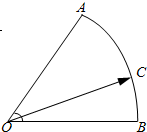    （2013•杭州一模）如图，在扇形OAB中，∠AOB=60°，点C为弧AB上的一个动点．若
    OC
    =x
    OA
    +y
    OB
    ，则x+3y的取值范围是
    [1，3]
    [1，3]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2002•上海）如图，三棱柱OAB-O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°，∠AOB=90°，且OB=OO1=2，OA=
    		3
    ，求
    （1）二面角O1-AB-O的大小；
    （2）异面直线A1B与AO1所成角的大小．（上述结果用反三角函数值表示）

    查看答案和解析>>

    同步练习册答案