
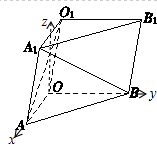
 (2002•上海)如图,三棱柱OAB-O1A1B1,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=
(2002•上海)如图,三棱柱OAB-O1A1B1,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=| 3 |
| AB |
| A1O |
| m |
| 3 |
| 3 |
| n |
| A1B |
| 3 |
| 3 |
| AO1 |
| 3 |
| 3 |
| A1B |
| AO1 |
| 3 |
| 3 |
| AB |
| 3 |
| AO1 |
| 3 |
| 3 |
| m |
|
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| n |
| m |
| n |
| ||||
|
| ||
|
| ||
| 4 |
| ||
| 4 |
| 3 |
| 3 |
| A1B |
| 3 |
| 3 |
| AO1 |
| 3 |
| 3 |
| A1B |
| AO1 |
| ||||
|
| 3+1-3 | ||||
|
| 1 |
| 7 |
| 1 |
| 7 |


科目:高中数学 来源: 题型:
 (2002•上海)如图所示,客轮以速度2v由A至B再到C匀速航行,货轮从AC的中点D出发,以速度v沿直线匀速航行,将货物送达客轮.已知AB=BC=50海里,若两船同时起航出发,则两船相遇之处距C点
(2002•上海)如图所示,客轮以速度2v由A至B再到C匀速航行,货轮从AC的中点D出发,以速度v沿直线匀速航行,将货物送达客轮.已知AB=BC=50海里,若两船同时起航出发,则两船相遇之处距C点查看答案和解析>>
科目:高中数学 来源: 题型:044
(2007
上海,18)近年来,太阳能技术运用的步伐日益加快.2002年全球太阳电池的年生产量达到670兆瓦,年生产量的增长率为34%.以后四年中,年生产量的增长率逐年递增2%(如2003年的年生产量的增长率为36%).(1)
求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦).(2)
目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?查看答案和解析>>
科目:高中数学 来源: 题型:
(07年上海卷)(14分)近年来,太阳能技术运用的步伐日益加快.2002年全球太阳电池的年生产量达到670兆瓦,年生产量的增长率为34%. 以后四年中,年生产量的增长率逐年递增2%(如,2003年的年生产量的增长率为36%).
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com