练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．函数$y=\frac{x}{{{x^2}+a}}$的图象不可能是（　　）
    A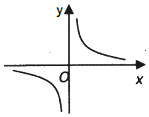．B．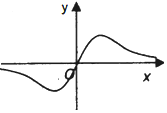
    C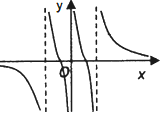．D．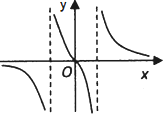

    分析 通过a的取值，判断函数的图象，推出结果即可．

    解答 解：当a=0时，函数化为y=$\frac{1}{x}$，函数的图象为：A；
    当a=1时，x=0时，y=0，x≠0时，函数化为y=$\frac{1}{x+\frac{1}{x}}$，函数的图象为：B；
    当a=-1时，函数化为y=$\frac{x}{{x}^{2}-1}$，当x∈（0，1）时，y′=$\frac{{x}^{2}-1-2{x}^{2}}{（{x}^{2}-1）^{2}}$＜0，函数是减函数，f（0）=0，可知函数的图象为：D；
    故选：C．

    点评 本题考查函数的单调性的应用，函数的导数的应用，赋值法的应用，考查转化思想以及计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．在△ABC中，角C=60°，tan$\frac{A}{2}$+tan$\frac{B}{2}$=1，则tan$\frac{A}{2}$•tan$\frac{B}{2}$=1-$\frac{\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．函数y=sin（3x+$\frac{π}{4}$）的图象适当变换就可以得到y=cos3x的图象，这种变换可以是（　　）
    A．向右平移$\frac{π}{4}$个单位长度B．向右平移$\frac{π}{12}$个单位长度
    C．向左平移$\frac{π}{4}$个单位长度D．向左平移$\frac{π}{12}$个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

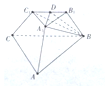    8．已知三棱台ABC-A1B1C1中，平面BB1C1C⊥平面ABC，∠ACB=90°，BB1=CC1=B1C1=2，BC=4，AC=6
    （1）求证：BC1⊥平面AA1C1C
    （2）点D是B1C1的中点，求二面角A1-BD-B1的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

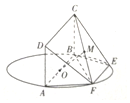    15．如图，AB为圆O的直径，点E，F在圆O上，AB∥EF，矩形ABCD所在的平面和圆（x-1）2+y2=1所在的平面互相垂直，且AB=2，AD=EF=1，∠BAF=60°．
    （1）求证：AF⊥平面CBF；
    （2）设FC的中点为M，求三棱锥M-DAF的体积V1与多面体CD-AFEB的体积V2之比的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=lnx+mx（m为常数）．
    （1）讨论函数f（x）的单调区间；
    （2）当$m≤-\frac{{3\sqrt{2}}}{2}$时，设$g（x）=f（x）+\frac{1}{2}{x^2}$的两个极值点x1，x2（x1＜x2）恰为h（x）=2lnx-ax-x2的零点，求$y=（{x_1}-{x_2}）h'（\frac{{{x_1}+{x_2}}}{2}）$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知$\frac{π}{2}＜α＜π$，3sin2α=2cosα，则$sin（α-\frac{9π}{2}）$=$\frac{2\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知0＜a＜b，且a+b=1，则下列不等式中正确的是（　　）
    A．log2a＞0B．2a-b＜$\frac{1}{2}$C．log2a+log2b＜-2D．2（$\frac{a}{b}$+$\frac{b}{a}$）＜$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知命题p：?x∈R，2x2+2x+$\frac{1}{2}$＜0，命题q：?x0∈R，sinx0-cosx0=$\sqrt{2}$，则下列判断中正确的是（　　）
    A．p是真命题B．q是假命题C．￢p是假命题D．￢q是假命题

    查看答案和解析>>

    同步练习册答案