练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位，再向上平移一个单位，所得函数图象对应的解析式为（　　）
    A．y=2sin2xB．y=2cos2xC．y=sin（2x-$\frac{π}{4}$）+1D．y=-cos2x

    分析 由条件利用诱导公式、函数y=Asin（ωx+φ）的图象变换规律，可得结论．

    解答 解：将函数y=sin2x的图象向右平移$\frac{π}{4}$个单位，可得函数y=sin2（x-$\frac{π}{4}$）=-cos2x 的图象，
    再向上平移一个单位，所得函数图象对应的解析式y=-cos2x+1=2sin2x，
    故选：A．

    点评 本题主要考查诱导公式的应用，函数y=Asin（ωx+φ）的图象变换规律，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．若随机变量X～N（1，4），则P（1＜X≤3）=（　　）
    （附：若随机变量X～N（μ，σ2）（σ＞0），则P（μ-σ＜X≤（μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544．
    A．0.6826B．0.3413C．0.9544D．0.4772

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=（ax2+x-1）ex，g（x）=$\frac{1}{3}$x3+$\frac{1}{2}$x2+m．
    （Ⅰ）当a＜0时，求函数f（x）的单调区间；
    （Ⅱ）当a=-1时，若函数h（x）=f（x）-g（x）有3个不同的零点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知A，B，C，D是以O为球心的球面上的四点，AB，AC，AD两两互相垂直，且AB=3，AC=4，AD=$\sqrt{11}$，则球的半径为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列结论正确的是（　　）
    A．若向量$\overrightarrow{a}$∥$\overrightarrow{b}$，则存在唯一实数λ使$\overrightarrow{a}$=λ$\overrightarrow{b}$
    B．“若θ=$\frac{π}{3}$，则cosθ=$\frac{1}{2}$”的否命题为“若θ≠$\frac{π}{3}$，则cosθ≠$\frac{1}{2}$”
    C．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$为非零向量，则“$\overrightarrow{a}$、$\overrightarrow{b}$的夹角为钝角”的充要条件是“$\overrightarrow{a}$$•\overrightarrow{b}$＜0”
    D．若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1＞0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知A={x|-x2+3x-2＞0}，B={x|x2-（a+1）x+a≤0}
    （Ⅰ）求B；
    （Ⅱ）若A?B时，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在△ABC中，角A、B、C所对的边为a、b、c，且A=120°，b=5，c=6，则a=9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．在直角坐标系xOy中，向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$的方向和长度如图所示，分别求它们的坐标．

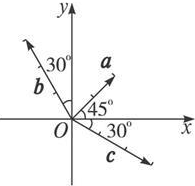
    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

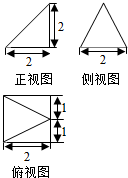    3．已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（　　）cm2．
    A．$\frac{4}{3}$B．$\frac{8}{3}$C．2D．4

    查看答案和解析>>

    同步练习册答案