
【题目】己知椭圆![]() 的焦距为
的焦距为![]() ,以椭圆C的右顶点A为圆心的圆与直线
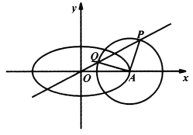
,以椭圆C的右顶点A为圆心的圆与直线![]() 相交于P,Q两点,且
相交于P,Q两点,且![]() .
.
(I)求椭圆C的标准方程和圆A的方程。
(II)不过原点的直线l与椭圆C交于M,N两点,已知直线OM,l,ON的斜率![]() 成等比数列,记以线段OM,线段ON为直径的圆的面积分别为
成等比数列,记以线段OM,线段ON为直径的圆的面积分别为![]() 的值是否为定值?若是,求出此值:若不是,说明理由.
的值是否为定值?若是,求出此值:若不是,说明理由.
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】手机是人们必不可少的工具,极大地方便了人们的生活、工作、学习,现代社会的衣食住行都离不开它.某调查机构调查了某地区各品牌手机的线下销售情况,将数据整理得如下表格:
品牌 |
|
|
|
|
|
| 其他 |
销售比 |
|
|
|
|
|
|
|
每台利润(元) | 100 | 80 | 85 | 1000 | 70 | 200 |
该地区某商场岀售各种品牌手机,以各品牌手机的销售比作为各品牌手机的售出概率.
(1)此商场有一个优惠活动,每天抽取一个数字![]() (
(![]() ,且
,且![]() ),规定若当天卖出的第
),规定若当天卖出的第![]() 台手机恰好是当天卖出的第一台
台手机恰好是当天卖出的第一台![]() 手机时,则此
手机时,则此![]() 手机可以打5折.为保证每天该活动的中奖概率小于0.05,求
手机可以打5折.为保证每天该活动的中奖概率小于0.05,求![]() 的最小值;(
的最小值;(![]() ,
,![]() )
)
(2)此商场中一个手机专卖店只出售![]() 和
和![]() 两种品牌的手机,
两种品牌的手机,![]() ,
,![]() 品牌手机的售出概率之比为
品牌手机的售出概率之比为![]() ,若此专卖店一天中卖出3台手机,其中
,若此专卖店一天中卖出3台手机,其中![]() 手机
手机![]() 台,求
台,求![]() 的分布列及此专卖店当天所获利润的期望值.
的分布列及此专卖店当天所获利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个结论:
①函数![]() 与函数
与函数![]() 的定义域相同,②函数
的定义域相同,②函数![]() (
(![]() 为常数)图像可由
为常数)图像可由![]() 的图像平移得到,③函数
的图像平移得到,③函数![]() 是奇函数且
是奇函数且![]() 是偶函数,④若幂函数
是偶函数,④若幂函数![]() 是奇函数,则
是奇函数,则![]() 是定义域上的增函数,其中正确的结论的序号是_________(将所有正确结论的序号都填上)
是定义域上的增函数,其中正确的结论的序号是_________(将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区为调查新生婴儿健康状况,随机抽取6名8个月龄婴儿称量体重(单位:千克),称量结果分别为6,8,9,9,9.5,10.已知8个月龄婴儿体重超过7.2千克,不超过9.8千克为“标准体重”,否则为“不标准体重”.
(1)根据样本估计总体思想,将频率视为概率,若从该地区全部8个月龄婴儿中任取3名进行称重,则至少有2名婴儿为“标准体重”的概率是多少?
(2)从抽取的6名婴儿中,随机选取4名,设X表示抽到的“标准体重”人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的余弦值是
所成角的余弦值是![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() :
:![]() 的焦点
的焦点![]() ,与抛物线
,与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点![]() 的两条直线
的两条直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() 和
和![]() 、
、![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() 、
、![]() .如果直线
.如果直线![]() 与
与![]() 的倾斜角互余,求证:直线
的倾斜角互余,求证:直线![]() 经过一定点.
经过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com