
 如图,O为原点,从椭圆
如图,O为原点,从椭圆| x2 |
| 100 |
| y2 |
| 4 |
| 23 |
| 23 |
科目:高中数学 来源:山东肥城六中2008届高中数学(新课标)模拟示范卷4 题型:013
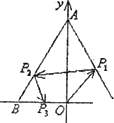
如图,在直角坐标系中,三角形ABC的顶点坐标分别为A(0,![]() ),B(-1,0),C(1,0),O为原点,从O点出发的光线先经AC上的点P1反射到边AB上,再由AB上的点P2反射回到BC边上的点P3停止,则光线OP1的斜率的范围为
),B(-1,0),C(1,0),O为原点,从O点出发的光线先经AC上的点P1反射到边AB上,再由AB上的点P2反射回到BC边上的点P3停止,则光线OP1的斜率的范围为
A.[![]() ,2
,2![]() ]
]
B.[![]() ,3
,3![]() ]
]
C.[![]() ,3
,3![]() ]
]
D.[![]() ,2
,2![]() ]
]
查看答案和解析>>
科目:高中数学 来源:2013届重庆市高二上学期期末理科数学试卷 题型:填空题
如图,O为原点,从椭圆 的左焦点F引圆
的左焦点F引圆 的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则
的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则 的值为_____________
的值为_____________

查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市西南大学附中高二(上)期末数学试卷(理科)(解析版) 题型:填空题
 的左焦点F引圆x2+y2=4的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则|MO|-|MT|的值为 .
的左焦点F引圆x2+y2=4的切线FT交椭圆于点P,切点T位于F、P之间,M为线段FP的中点,M位于F、T之间,则|MO|-|MT|的值为 .
查看答案和解析>>
科目:高中数学 来源:0103 模拟题 题型:填空题
 的左焦点F1引圆的切线F1T交椭圆于点P,切点T位于F1,P之间,M为线段F1P的中点,则|MO|-|MT|的值为( )。
的左焦点F1引圆的切线F1T交椭圆于点P,切点T位于F1,P之间,M为线段F1P的中点,则|MO|-|MT|的值为( )。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com