
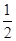 ,求a及此时f(x)的最大值.
,求a及此时f(x)的最大值.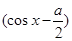 2-
2-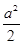 -2a-1.-1≤cosx≤1.转化为二次函数问题解决.
-2a-1.-1≤cosx≤1.转化为二次函数问题解决.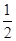 ,建立关于a的方程求解即可.
,建立关于a的方程求解即可.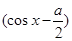 2-
2-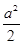 -2a-1.这里-1≤cosx≤1. …………4分
-2a-1.这里-1≤cosx≤1. …………4分 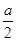 ≤1,即-2≤a≤2,则当cosx=
≤1,即-2≤a≤2,则当cosx=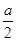 时,f(x)min=-
时,f(x)min=-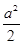 -2a-1;…………5分
-2a-1;…………5分 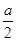 >1,则当cosx=1时,f(x)min=1-4a;…………6分
>1,则当cosx=1时,f(x)min=1-4a;…………6分 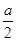 <-1,则当cosx=-1时,f(x)min=1. …………7分
<-1,则当cosx=-1时,f(x)min=1. …………7分 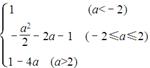 .…………8分
.…………8分 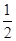 .
.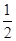 ,得a=
,得a=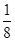 ,矛盾; …………10分
,矛盾; …………10分 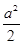 -2a-1=
-2a-1=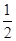 ,
,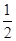 时,a=-1. 此时f(x)=2
时,a=-1. 此时f(x)=2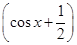 2+
2+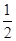 ,
, 

科目:高中数学 来源:不详 题型:解答题
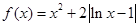 .
.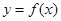 的最小值;
的最小值;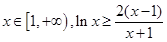 恒成立;
恒成立;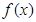 图象上的不同两点
图象上的不同两点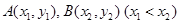 ,如果在函数
,如果在函数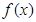 图象上存在点
图象上存在点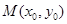 (其中
(其中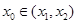 )使得点
)使得点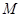 处的切线
处的切线 ,则称直线
,则称直线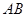 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当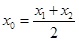 时,又称直线
时,又称直线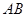 存在 “中值伴侣切线”.试问:当
存在 “中值伴侣切线”.试问:当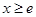 时,对于函数
时,对于函数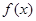 图象上不同两点
图象上不同两点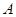 、
、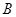 ,直线
,直线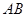 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
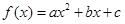 (a>0),方程
(a>0),方程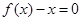 的两个根
的两个根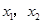
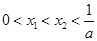 . (1)
. (1)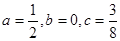 ,求
,求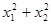 的值。
的值。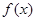 的图象关于直线
的图象关于直线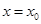 对称,证明:
对称,证明: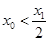
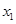 )时,证明x<
)时,证明x<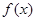 <
<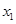 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com