练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在1与2之间插入6个正数，使这8个数成等比数列，则插入的6个数的积为8．

    分析 等比数列的性质即可得出．

    解答 解：根据等比数列的性质可得：插入的6个数的积=（1×2）3=8．
    故答案为：8．

    点评 本题考查了等比数列的性质，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．设函数$f（x）=\left\{\begin{array}{l}\frac{1}{2}x-1，x＞0\\{（{\frac{1}{2}}）^x}，x≤0\end{array}\right.$，若f（a）=1，则实数a的值等于0或4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．构造如图所示的数表，规则如下：先排两个1作为第一层，然后在每一层的相邻两个数之间插入这两个数和的a倍得下一层，其中a＞0，设n层中有an个数，这an个数的和为Sn（n∈N*）．
    （1）求an；
    （2）求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数y=$\frac{4sinxcosx}{2sinx+2cosx+1}$，x∈（0，$\frac{π}{2}$）．
    （1）令t=sinx+cosx，可将已知三角函数关系y=f（x）转换成代数函数关系y=g（t），试写出函数y=g（t）的表达式及定义域；
    （2）求函数y=f（x）的最大值；
    （3）函数y=f（x）在区间（0，$\frac{π}{2}$）内是单调函数吗？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知角α终边上有一点P到原点的距离为4，α=60°，则点P的坐标是（2，2$\sqrt{3}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．求下列各函数的定义域．
    （1）y=x${\;}^{-\frac{3}{2}}$；
    （2）y=$\sqrt{9-{3}^{x}}$；
    （3）y=1n（3x+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数$f（x）=|{\frac{1}{2}x+1}|+|{x-1}|（x∈R）$的最小值为a．
    （1）求a；
    （2）已知两个正数m，n满足m2+n2=a，求$\frac{1}{m}+\frac{1}{n}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

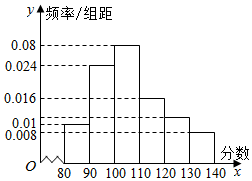    2．某校在2 015年11月份的高三期中考试后，随机地抽取了50名学生的数学成绩并进行了分析，结果这50名同学的成绩全部介于80分到140分之间．现将结果按如下方式分为6组，第一组[80，90），第二组[90，100），…第六组[130，140]，得到如图所示的频率分布直方图．
    （Ⅰ）试估计该校数学的平均成绩（同一组中的数据用该区间的中点值作代表）；
    （Ⅱ）这50名学生中成绩在120分以上的同学中任意抽取3人，该3人在130分（含130分）以上的人数记为X，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

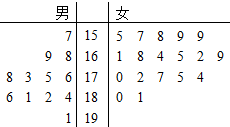    3．某小学对五年级的学生进行体质测试，已知五年一班共有学生30人，测试立定跳远的成绩用茎叶图表示如图（单位：cm）：
    男生成绩在175cm以上（包括175cm）定义为“合格”，成绩在175cm以下（不包括175cm）定义为“不合格”．
    女生成绩在165cm以上（包括165cm）定义为“合格”，成绩在165cm以下（不包括165cm）定义为“不合格”．
    （Ⅰ）求五年一班的女生立定跳远成绩的中位数；
    （Ⅱ）在五年一班的男生中任意选取3人，求至少有2人的成绩是合格的概率；
    （Ⅲ）若从五年一班成绩“合格”的学生中选取2人参加复试，用X表示其中男生的人数，写出X的分布列，并求X的数学期望．

    查看答案和解析>>

    同步练习册答案