
 已知函数
已知函数 (其中ω>0),且函数f(x)的图象的相邻两条对称轴间的距离为π.
(其中ω>0),且函数f(x)的图象的相邻两条对称轴间的距离为π.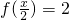 ,求
,求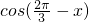 的值.
的值. =
= sin2ωx+cos2ωx+1=2sin(2ωx+
sin2ωx+cos2ωx+1=2sin(2ωx+ )+1,
)+1, •
• =π,解得ω=
=π,解得ω= ,∴f(x)=2sin(x+
,∴f(x)=2sin(x+ )+1.
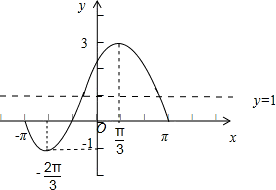
)+1. x+ | - | - | 0 |  | π |  |
| x | -π | - | - |  |  | π |
| f(x) | 0 | -1 | 1 | 3 | 1 | 0 |
 . 又B为三角形的内角,∴B=
. 又B为三角形的内角,∴B= .
. ,0<A<
,0<A< ,
, <A+
<A+ <
< ,
, <sin(A+
<sin(A+ )≤1,故函数f(A)=2sin(A+
)≤1,故函数f(A)=2sin(A+ )+1 的取值范围为(2,3].
)+1 的取值范围为(2,3]. )=2sin(
)=2sin( +
+ )+1=2,∴sin(
)+1=2,∴sin( +
+ )=
)= ,
, -x)=2
-x)=2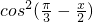 -1=2
-1=2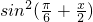 -1=2×
-1=2× -1=-
-1=- .
. )+1,由周期求得ω的值,即可确定f(x)的解析式为 2sin(x+
)+1,由周期求得ω的值,即可确定f(x)的解析式为 2sin(x+ )+1,列表作出它的图象.
)+1,列表作出它的图象. 0=2,求得sin(
0=2,求得sin( +
+ )=
)= ,再利用二倍角公式、诱导公式求得 cos(
,再利用二倍角公式、诱导公式求得 cos( -x)=2
-x)=2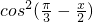 -1 的值.
-1 的值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2010-2011学年黑龙江省大庆实验中学高一(上)期中数学试卷(解析版) 题型:解答题
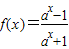 ,其中a>0且a≠1.
,其中a>0且a≠1.查看答案和解析>>
科目:高中数学 来源:2013年北京市西城区高考数学二模试卷(文科)(解析版) 题型:解答题
 ,其中a>0.
,其中a>0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com