练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    y=5sin（2x+θ）的图象关于y轴对称，则θ=    ．
    【答案】分析：根据函数y=f（x）为偶函数得到f（-x）=f（x），然后代入到解析式中根据两角和与差的正弦公式展开，最后根据三角函数的性质确定答案．
    解答：解：∵y=f（x）为偶函数
    ∴5sin（2x+θ）=5sin（-2x+θ）
    ∴sin2xcosθ+cos2xsinθ=-sin2xcosθ+cos2xsinθ
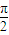
    ∴sin2xcosθ=0∴cosθ=0∴θ=kπ+（k∈Z）
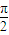
    故答案为：kπ+（k∈Z）
    点评：本题主要考查两角和与差的正弦公式和三角函数的性质--奇偶性．考查综合运用能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    y=5sin（2x+θ）的图象关于y轴对称，则θ=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将函数y=sin(2x+
    π
    3
    )    的图象向右移
    π
    6
    个单位所得函数解析式是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    把函数y=5sin(2x-
    π
    6
    )    图象上所有点的横坐标伸长为原来的2倍（纵坐标不变），再把所得函数的图象向右平移
    π
    3
    个单位，得到图象的解析式为（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    y=5sin（2x+θ）的图象关于y轴对称，则θ=______．

    查看答案和解析>>

    同步练习册答案