
如图,已知⊙O中∠AOB=2∠BOC,求证:∠ACB=2∠BAC.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:
 如图,已知E、F为平面上的两个定点|EF|=6,|FG|=10,且2
如图,已知E、F为平面上的两个定点|EF|=6,|FG|=10,且2| EH |
| EG |
| HP |
| GE |
| 9 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
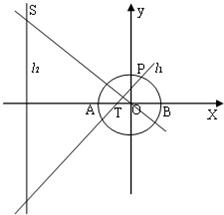 如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.
如图,已知圆O:x2+y2=2交x轴于A、B两点,P在圆O上运动(不与A、B重合),过P作直线l1,OS垂直于l1交直线l2:x=-3于点S.| OP |
| PS |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )
如图,已知函数y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),若随机向圆O:x2+y2=π2内投入一米粒,则该米粒落在区域M内的概率是( )查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分. |
| BD |
| GF |
| AG |
| EF2 |
| CE2 |
查看答案和解析>>
科目:高中数学 来源:2013年吉林省长春市高考数学一模试卷(理科)(解析版) 题型:解答题
 中点,连接AG分别交⊙O、BD于点E、F,连接CE.
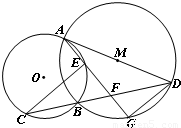
中点,连接AG分别交⊙O、BD于点E、F,连接CE.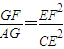 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com