
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县新海高级中学高三(上)10月学情调研数学试卷(文科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的右焦点为F(4m,0)(M>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(M>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点. +
+ =
= ,求实数m;
,求实数m; +
+ 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省成都市新都一中高一(上)数学测试卷(9)(解析版) 题型:解答题
 、
、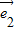 满足
满足 ,
, ,且
,且 、
、 的夹角为60°,设向量
的夹角为60°,设向量 与向量
与向量 的夹角为θ(t∈R).
的夹角为θ(t∈R).查看答案和解析>>
科目:高中数学 来源:2011年福建省莆田市高三质量检查数学试卷(理科)(解析版) 题型:解答题


查看答案和解析>>
科目:高中数学 来源:2010年上海市闸北区高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com