
科目:高中数学 来源:不详 题型:解答题
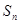 是数列
是数列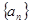 的前
的前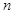 项和,
项和,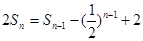 (
(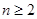 ,
,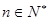 ),且
),且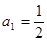 .
.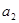 的值,并写出
的值,并写出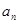 和
和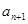 的关系式;
的关系式;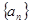 的通项公式及
的通项公式及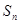 的表达式;
的表达式; 3)我们可以证明:若数列
3)我们可以证明:若数列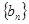 有上界(即存在常数
有上界(即存在常数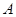 ,使得
,使得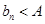 对一切
对一切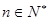 恒成立)且单调递增;或数列
恒成立)且单调递增;或数列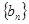 有下界(即存在常数
有下界(即存在常数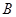 ,使得
,使得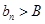 对一切
对一切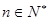 恒成立)且单调递减,则
恒成立)且单调递减,则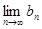 存在.直接利用上述结论,证明:
存在.直接利用上述结论,证明: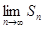 存在.
存在. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
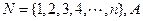 为非空集合,且
为非空集合,且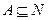 ,定义
,定义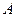 的“交替和”如下:将集合
的“交替和”如下:将集合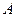 中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合
中的元素按由大到小排列,然后从最大的数开始,交替地减、加后续的数,直到最后一个数,并规定单元素集合的交替和为该元素。例如集合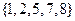 的交替和为8-7+5-2+1=5,集合
的交替和为8-7+5-2+1=5,集合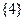 的交替和为4,当
的交替和为4,当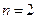 时,集合
时,集合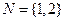 的非空子集为
的非空子集为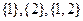 ,记三个集合的交替和的总和为
,记三个集合的交替和的总和为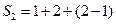 = 4,则
= 4,则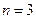 时,集合
时,集合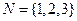 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和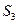 = ;集合
= ;集合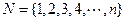 的所有非空子集的交替和的总和
的所有非空子集的交替和的总和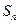 =
= 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
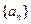 中,如果存在非零的常数
中,如果存在非零的常数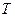 ,使得
,使得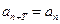 对于任意正整数
对于任意正整数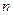 均成立,那么就称数列
均成立,那么就称数列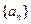 为周期数列,其中
为周期数列,其中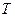 叫做数列
叫做数列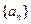 的周期. 已知数列
的周期. 已知数列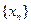 满足
满足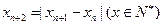 ,若
,若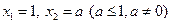 ,当数列
,当数列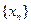 的周期为
的周期为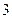 时,则数列
时,则数列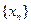 的前
的前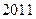 项的和
项的和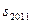 为( )
为( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com