
(08年安徽卷理) (本小题满分13分)
设椭圆![]() 过点
过点![]() ,且左焦点为
,且左焦点为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于两不同点
相交于两不同点![]() 时,在线段
时,在线段![]() 上取点
上取点![]() ,满足
,满足![]() 。证明:点Q总在某定直线上。
。证明:点Q总在某定直线上。
【解析】本题主要考查直线、椭圆的方程及几何性质、线段的定比分点等基础知识、基本方法和分析问题、解决问题的能力.本小题满分13分.(Ⅰ)由题意: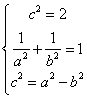 ,解得
,解得![]() .
.
所求的求椭圆![]() 的方程
的方程![]() .
.
(Ⅱ)方法一:设点![]() ,
,![]() ,
,![]() ,由题设,
,由题设,![]() 、
、![]() 、
、![]() 、
、![]() 均不为0,且
均不为0,且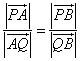 ,又
,又![]() 四点共线,可设
四点共线,可设![]() ,
,![]() ,于是
,于是
![]() ,
,![]() …………………………………①
…………………………………①
![]() ,
,![]() …………………………………②
…………………………………②
由于![]() ,
,![]() 在椭圆上,将①②分别带入
在椭圆上,将①②分别带入![]() 的方程
的方程![]() ,整理得:
,整理得:
![]() ………………③
………………③
![]() ………………④
………………④
由④-③得 ![]() .
.
∵![]() ,∴
,∴![]() .即点
.即点![]() 总在直线
总在直线![]() 上.
上.
方法二:设点![]() ,
,![]() ,
,![]() ,由题设,
,由题设,![]() 、
、![]() 、
、![]() 、
、![]() 均不为0,记
均不为0,记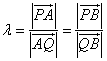 ,则
,则![]() 且
且![]() .
.
又![]() 四点共线,从而
四点共线,从而![]() ,
,![]() ,于是:
,于是:
![]() ,
,![]() ;
;
![]() ,
,![]() .
.
从而![]() ……………①
……………① ![]() ……………②
……………②
又点![]() 在椭圆上,即
在椭圆上,即
![]() ………………③
………………③
![]() ………………④
………………④
①+2![]() ②并结合③,④得
②并结合③,④得![]() ,即点
,即点![]() 总在直线
总在直线![]() 上.
上.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
(08年安徽卷理)(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了![]() 株沙柳。各株沙柳的成活与否是相互独立的,成活率为
株沙柳。各株沙柳的成活与否是相互独立的,成活率为![]() ,设
,设![]() 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望![]() 为3,标准差
为3,标准差![]() 为
为![]() 。
。
(Ⅰ)求![]() 的值,并写出
的值,并写出![]() 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽卷理)(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了![]() 株沙柳。各株沙柳的成活与否是相互独立的,成活率为
株沙柳。各株沙柳的成活与否是相互独立的,成活率为![]() ,设
,设![]() 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望![]() 为3,标准差
为3,标准差![]() 为
为![]() 。
。
(Ⅰ)求![]() 的值,并写出
的值,并写出![]() 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年安徽卷理)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 底面
底面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
(I)证明:直线![]() 平面
平面![]() .
.
(II)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
(III)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com