
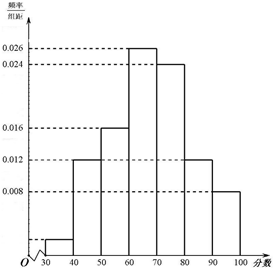
 学业水平考试(满分为100分)中,成绩在[80,100]为A等,在[60,80)为B等,在[40,60)为C等,不到40分为D等.某校高二年级共有1200名学生,其中男生720名,女生480名,该校组织了一次物理学业水平模拟考试.为研究这次物理考试成绩为A等是否与性别有关,现按性别采用分层抽样抽取100名学生的成绩,按从低到高分成[30,40),[40,50),[60,70),[70,80),[80,90),[90,100]七组,并绘制成如图所示的频率分布直方图.
学业水平考试(满分为100分)中,成绩在[80,100]为A等,在[60,80)为B等,在[40,60)为C等,不到40分为D等.某校高二年级共有1200名学生,其中男生720名,女生480名,该校组织了一次物理学业水平模拟考试.为研究这次物理考试成绩为A等是否与性别有关,现按性别采用分层抽样抽取100名学生的成绩,按从低到高分成[30,40),[40,50),[60,70),[70,80),[80,90),[90,100]七组,并绘制成如图所示的频率分布直方图.| 物理成绩为A等 | 物理成绩不为A等 | 合计 | |
| 男生 | a=14 | b=46 | |
| 女生 | c=6 | d=34 | |
| 合计 | n=100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
分析 (1)利用频率分布直方图中的数据,求出成绩为D等的概率,然后求解成绩为D等的人数.
(2)由列联表中数据,代入公式,求出K2的值,进而与临界值比较,即可得出结论.
解答 解:(1)设抽取的100名学生中,本次考试成绩为D等的有x人,根据题意得x=100×[1-10×(0.006+0.012×2+0.018+0.024+0.026)]=2,
据此估计该校高二年级学生在物理学业水平考试中,成绩为D等的人数为$\frac{2}{100}×1200$=24(人)…(4分)
(2)根据已知条件得列联表如下:
| 物理成绩为A等 | 物理成绩不为A等 | 合计 | |
| 男生 | a=14 | b=46 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 20 | 80 | n=100 |
点评 本题考查独立性检验的应用,考查数据处理能力、运算求解能力和应用意识,本题解题的关键是正确运算出观测值,理解临界值对应的概率的意义,要想知道两个变量之间的有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能做出判断,本题是一个基础题.


科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{CD}$,$\overrightarrow{BC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{OD}$=$\overrightarrow{OA}$ | C. | $\overrightarrow{AO}$+$\overrightarrow{OD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{DA}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2π | B. | 2 | C. | 4π | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
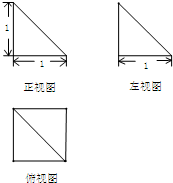
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com