
| A. | [1,+∞) | B. | (-∞,1] | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
分析 由函数f(x)=x3+sinx,利用函数f(x)的奇偶性与单调性.不等式f(msinθ)+f(1-m)>0恒成立,转化为:msinθ>m-1,再利用0<θ<$\frac{π}{2}$,0<sinθ<1,即可得出实数m的取值范围.
解答 解:∵函数f(x)=x3+sinx,则f(-x)=-f(x),则函数f(x)是奇函数.
当0<θ<$\frac{π}{2}$时,f′(x)=3x2+cosx>0,函数f(x)单调递增.
不等式f(msinθ)+f(1-m)>0恒成立,转化为:f(msinθ)>-f(1-m)=f(m-1),
∴msinθ>m-1,
∴m<$\frac{1}{1-sinθ}$恒成立.
∵由0<θ<$\frac{π}{2}$知,0<sinθ<1,0<1-sinθ<1,$\frac{1}{1-sinθ}$>1,
∴m≤1.
∴实数m的取值范围是(-∞,1].
故选:B.
点评 本题考查了利用导数研究其单调性极值与最值、不等式的性质、三角函数的值域、函数的性质,考查了分类讨论、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 存在x≤0,使得 ex<1 | B. | 存在x>0,使得 ex<1 | ||
| C. | 任意x>0,总有 ex<1 | D. | 任意x≤0,总有 ex<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰梯形 | B. | 矩形 | C. | 正方形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
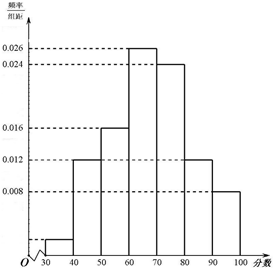 学业水平考试(满分为100分)中,成绩在[80,100]为A等,在[60,80)为B等,在[40,60)为C等,不到40分为D等.某校高二年级共有1200名学生,其中男生720名,女生480名,该校组织了一次物理学业水平模拟考试.为研究这次物理考试成绩为A等是否与性别有关,现按性别采用分层抽样抽取100名学生的成绩,按从低到高分成[30,40),[40,50),[60,70),[70,80),[80,90),[90,100]七组,并绘制成如图所示的频率分布直方图.
学业水平考试(满分为100分)中,成绩在[80,100]为A等,在[60,80)为B等,在[40,60)为C等,不到40分为D等.某校高二年级共有1200名学生,其中男生720名,女生480名,该校组织了一次物理学业水平模拟考试.为研究这次物理考试成绩为A等是否与性别有关,现按性别采用分层抽样抽取100名学生的成绩,按从低到高分成[30,40),[40,50),[60,70),[70,80),[80,90),[90,100]七组,并绘制成如图所示的频率分布直方图.| 物理成绩为A等 | 物理成绩不为A等 | 合计 | |
| 男生 | a=14 | b=46 | |
| 女生 | c=6 | d=34 | |
| 合计 | n=100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com