
分析 a+b+c=0,可得:a3+b3+c3=(a+b)3+c3-3ab(a+b)=3abc.代入化简即可得出.
解答 解:∵a+b+c=0,
∴a3+b3+c3=(a+b)3+c3-3ab(a+b)=-c3+c3-3ab(a+b)=3abc.
∴a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)+3=$\frac{a(b+c)}{bc}$+$\frac{b(a+c)}{bc}$+$\frac{c(a+b)}{ab}$+3=$\frac{-{a}^{3}-{b}^{3}-{c}^{3}}{abc}$+3=$\frac{-3abc}{abc}$+3=0.
点评 本题考查了代数式的化简与计算,考查了推理能力与计算能力,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | ($\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$=$\overrightarrow{CD}$,$\overrightarrow{BC}$=$\overrightarrow{AD}$ | B. | $\overrightarrow{AD}$+$\overrightarrow{OD}$=$\overrightarrow{OA}$ | C. | $\overrightarrow{AO}$+$\overrightarrow{OD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$ | D. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{DA}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
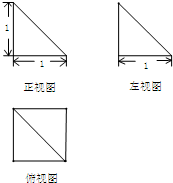
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com