
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
分析 求函数的导数,判断函数的单调性,利用函数单调性将不等式恒成立进行转化,结合一元二次不等式恒成立的性质进行求解即可.
解答 解:∵定义在R上的奇函数f(x)满足:当x≥0时,f(x)=x-sinx,
∴f(0)=0,且f′(x)=1-cosx≥0,即函数f(x)在[0,+∞)上为增函数,
∵f(x)是奇函数,∴函数f(x)在(-∞,0]上也是增函数,
即函数f(x)在(-∞,+∞)上为增函数,
则不等式f(-4t)>f(2m+mt2)等价为-4t>2m+mt2对任意实数t恒成立
即mt2+4t+2m<0对任意实数t恒成立,
若m=0,则不等式等价为4t<0,即t<0,不满足条件.,
若m≠0,则要使mt2+4t+2m<0对任意实数t恒成立,
则$\left\{\begin{array}{l}{m<0}\\{△=16-8{m}^{2}<0}\end{array}\right.$,即$\left\{\begin{array}{l}{m<0}\\{{m}^{2}>2}\end{array}\right.$,得m<-$\sqrt{2}$,
故选:A.
点评 本题主要考查不等式恒成立问题,根据条件判断函数的单调性,将不等式恒成立进行转化是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 等腰梯形 | B. | 矩形 | C. | 正方形 | D. | 菱形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=\sqrt{3}y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{{\sqrt{3}}}{3}y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=4x\\ y'=3y\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x′=\frac{1}{4}x}\\{y′=\frac{1}{3}y}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
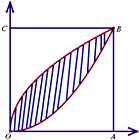 如图,在正方形OABC内,阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1)围成,在正方形内随机取一点,且此点取自阴影部分的概率是a,则函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x≥a)}\\{(\frac{1}{3})^{x}(x<a)}\end{array}\right.$的值域为[-1,+∞).
如图,在正方形OABC内,阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1)围成,在正方形内随机取一点,且此点取自阴影部分的概率是a,则函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x≥a)}\\{(\frac{1}{3})^{x}(x<a)}\end{array}\right.$的值域为[-1,+∞).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
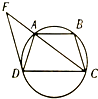 如图,已知梯形ABCD内接于圆O,AB∥CD,过点D作圆的切线交CA的延长线于点F,且DF∥BC,如果CA=5,BC=4.
如图,已知梯形ABCD内接于圆O,AB∥CD,过点D作圆的切线交CA的延长线于点F,且DF∥BC,如果CA=5,BC=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com