
| A. | $\left\{\begin{array}{l}x'=2x\\ y'=\sqrt{3}y\end{array}\right.$ | B. | $\left\{\begin{array}{l}x'=\frac{1}{2}x\\ y'=\frac{{\sqrt{3}}}{3}y\end{array}\right.$ | C. | $\left\{\begin{array}{l}x'=4x\\ y'=3y\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x′=\frac{1}{4}x}\\{y′=\frac{1}{3}y}\end{array}\right.$ |
分析 设伸缩变换φ为$\left\{\begin{array}{l}x'=hx\\ y'=ky\end{array}\right.,(h,k>0)$,代入$\frac{x^2}{4}+\frac{y^2}{3}=1$,化简计算即可得到.
解答 解:设伸缩变换φ为$\left\{\begin{array}{l}x'=hx\\ y'=ky\end{array}\right.,(h,k>0)$,
则$\left\{\begin{array}{l}x=\frac{x'}{h}\\ y=\frac{y'}{k}\end{array}\right.$,
代入$\frac{x^2}{4}+\frac{y^2}{3}=1$
得$\frac{x^2}{{4{h^2}}}+\frac{y^2}{{3{k^2}}}=1$,
∴$\left\{\begin{array}{l}4{h^2}=1\\ 3{k^2}=1\end{array}\right.⇒\left\{\begin{array}{l}h=\frac{1}{2}\\ k=\frac{{\sqrt{3}}}{3}\end{array}\right.$
故选:B
点评 本题考查了伸缩变换,关键是对变换公式的理解与运用,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{e}{2}}$) | B. | (1,$\frac{e}{2}}$] | C. | (-∞,0)∪(1,$\frac{e}{2}}$] | D. | (-∞,0)∪(1,$\frac{e}{2}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |r|趋近于0时,没有非线性相关关系 | B. | |r|越接近于1时,线性相关程度越强 | ||
| C. | |r|越大,相关程度越大 | D. | |r|越小,相关程度越大 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{2}$) | B. | (-$\sqrt{2}$,0) | C. | (-∞,0)∪($\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
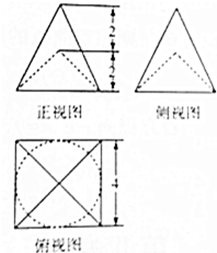
| A. | $\frac{192-8π}{3}$ | B. | $16+16\sqrt{5}+4(\sqrt{2}-1)π$ | C. | $\frac{56π}{3}$ | D. | $\frac{64-8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com