
【题目】如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在PD上.
,PA=2,点M在PD上. 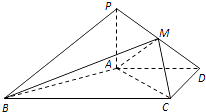
(1)求证:AB⊥PC
(2)若二面角M﹣AC﹣D的大小为45°,求 ![]() 的值.
的值.
【答案】
(1)证明:如图,设E为BC的中点,连结AE,
则AD=EC,AD∥EC,AD∥EC,所以四边形AECD为平行四边形,
故AE⊥BC,又AE=BE=EC=2 ![]() ,
,
所以∠ABC=∠ACB=45°,故AB⊥AC,
又因为PA⊥平面ABCD,所以AB⊥PA,
且PA∩AC=A,所以AB⊥平面PAC,故有AB⊥PC.
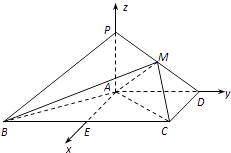
(2)解:如图,以A为原点,分别以射线AE、AD、AP为x,y,z轴的正半轴,建立空间直角坐标系A﹣xyz.
则A(0,0,0),E(2 ![]() ,0,0),B(2
,0,0),B(2 ![]() ,﹣2
,﹣2 ![]() ,0),C(2
,0),C(2 ![]() ,2
,2 ![]() ,0),D(0,2
,0),D(0,2 ![]() ,0),P(0,0,2),
,0),P(0,0,2),
设 ![]() =λ
=λ ![]() =(0,2
=(0,2 ![]() ,﹣2λ),(0≤λ≤1),解得M(0,2
,﹣2λ),(0≤λ≤1),解得M(0,2 ![]() ,2﹣2λ)
,2﹣2λ)
设平面AMC的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 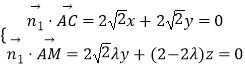 ,
,
令y= ![]() ,得
,得 ![]() ,即
,即 ![]()
又平面ACD的一个法向量为 ![]() ,
,
由题知  =
= ![]() ,
,
解得 ![]() .
.
∴ ![]() 的值为
的值为 ![]()
【解析】(1)设E为BC的中点,连结AE,推导出四边形AECD为平行四边形,AB⊥AC,AB⊥PA,由此能证明AB⊥PC.(2)以A为原点,分别以射线AE、AD、AP为x,y,z轴的正半轴,建立空间直角坐标系A﹣xyz.利用向量法能求出 ![]() 的值.
的值.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径. 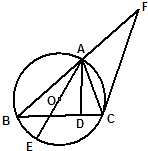
(1)求证:ACBC=ADAE;
(2)过点C作⊙O的切线交BA的延长线于点F,若AF=3,CF=9,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣3x,则函数g(x)=f(x)﹣x+3的零点的集合为( )
A.{1,3}
B.{﹣3,﹣1,1,3}
C.{2﹣ ![]() ,1,3}
,1,3}
D.{﹣2﹣ ![]() ,1,3}
,1,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,椭圆C上任意一点到椭圆左右两个焦点的距离之和为4.
(1)求椭圆C的方程;
(2)椭圆C与X轴负半轴交于点A,直线过定点(﹣1,0)交椭圆于M,N两点,求△AMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:

(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程![]() ,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式: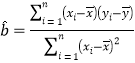 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com