
【题目】在图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有 . (填上所有正确答案的序号) 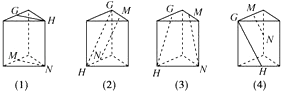
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在PD上.
,PA=2,点M在PD上. 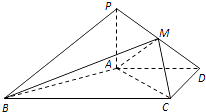
(1)求证:AB⊥PC
(2)若二面角M﹣AC﹣D的大小为45°,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
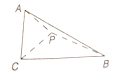
【题目】已知直角三角形![]() 的两条直角边
的两条直角边![]() ,
, ![]() ,
, ![]() 为斜边
为斜边![]() 上一点,沿
上一点,沿![]() 将三角形折成直二面角
将三角形折成直二面角![]() ,此时二面角
,此时二面角![]() 的正切值为
的正切值为![]() ,则翻折后
,则翻折后![]() 的长为( )
的长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数f(x)满足:
①对任意x,y∈R,都有:f(x+y)=f(x)+f(y)﹣1;
②当x<0时,f(x)>1.
(Ⅰ)试判断函数f(x)﹣1的奇偶性;
(Ⅱ)试判断函数f(x)的单调性;
(Ⅲ)若不等式f(a2﹣2a﹣7)+ ![]() >0的解集为{a|﹣2<a<4},求f(5)的值.
>0的解集为{a|﹣2<a<4},求f(5)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点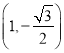 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2-e2x.
(1)若曲线y=f(x)在点(2,f(2))处的切线平行于x轴,求函数f(x)的单调区间;
(2)若x>0时,总有f(x)>-e2x,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,又数列{ ![]() }(n∈N*)是公差为1的等差数列.
}(n∈N*)是公差为1的等差数列.
(1)求数列{an}的通项公式an;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com