
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
【答案】(1)1(2)16
【解析】试题分析:(1)根据抛物线定义得![]() ,设
,设![]() ,利用同一法可得切点弦AB方程
,利用同一法可得切点弦AB方程![]() .联立切点弦方程与抛物线方程,利用韦达定理代入可得
.联立切点弦方程与抛物线方程,利用韦达定理代入可得![]() 的值;(2)
的值;(2)![]() ,
, ![]() 的方程为
的方程为![]() .
. ![]() ,联立切点弦方程与抛物线方程,利用韦达定理代入可得
,联立切点弦方程与抛物线方程,利用韦达定理代入可得![]() 的值.
的值.
试题解析:解:因为抛物线的方程为![]() ,所以
,所以![]() , 所以切线
, 所以切线![]() 的方程为
的方程为![]() ,即
,即![]() ①,同理切线
①,同理切线![]() 的方程为
的方程为![]() ②,设
②,设![]() ,则由①②得
,则由①②得![]() 以及
以及![]() ,由此得直线
,由此得直线![]() 的方程为
的方程为![]() .
.
(1)由于点![]() 是直线
是直线![]() 上的一个动点,所以
上的一个动点,所以![]() ,即直线
,即直线![]() 的方程为
的方程为![]() ,因此它过抛物线的焦点
,因此它过抛物线的焦点![]() .
.
当![]() 时,
时, ![]() 的方程为
的方程为![]() ,此时
,此时![]() ,所以
,所以![]() ;
;
当![]() 时,把直线
时,把直线![]() 方程代入抛物线方程得到
方程代入抛物线方程得到![]() ,从而有
,从而有![]() ,所以
,所以![]() .
.
综上, ![]() .
.
(2)由(1)知切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,联立得点
,联立得点![]()
![]() .
.
设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]() .因此
.因此![]()
![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() ,由题意
,由题意
![]() ,所以
,所以![]() ,从而
,从而![]()
![]()
![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:

(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;
(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程![]() ,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.
参考公式: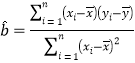 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知椭圆![]() 的右焦点为
的右焦点为![]() ,以椭圆
,以椭圆![]() 与双曲线
与双曲线![]() 两条渐近线的四个交点为顶点的四边形的面积为
两条渐近线的四个交点为顶点的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 为椭圆
为椭圆![]() 上的两点(
上的两点(![]() 不同时在
不同时在![]() 轴上),点
轴上),点![]() ,证明:存在实数
,证明:存在实数![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 为常数.
为常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12m2的背面靠墙的矩形小房子,由于地理位置的限制,房子侧面的长度x不得超过am.房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为正方形,
为正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
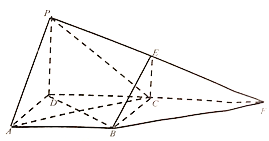
(1)若![]() 和
和![]() 延长交于点
延长交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 边上的动点,求直线
边上的动点,求直线![]() 与平面
与平面![]() 所成角正弦值的最小值.
所成角正弦值的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=(x﹣a)2+|x﹣a|﹣a(a﹣1).
(1)若f(0)≤1,求a的取值范围;
(2)求f(x)在R上的单调区间(无需使用定义严格证明,但必须有一定的推理过程);
(3)当a>2时,求函数g(x)=f(x)+|x|在R上的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com