
【题目】设a为实数,函数f(x)=(x﹣a)2+|x﹣a|﹣a(a﹣1).
(1)若f(0)≤1,求a的取值范围;
(2)求f(x)在R上的单调区间(无需使用定义严格证明,但必须有一定的推理过程);
(3)当a>2时,求函数g(x)=f(x)+|x|在R上的零点个数.
【答案】
(1)解:f(0)=a2+|a|﹣a2+a=|a|+a,因为f(0)≤1,所以|a|+a≤1,
当a≤0时,0≤1,显然成立;当a>0,则有2a≤1,所以 ![]() .所以
.所以 ![]() .
.
综上所述,a的取值范围是 ![]()
(2)解:  ,
,
对于y=x2﹣(2a﹣1)x,其对称轴为 ![]() ,开口向上,
,开口向上,
所以f(x)在(a,+∞)上单调递增;
对于y=x2﹣(2a+1)x,其对称轴为 ![]() ,开口向上,
,开口向上,
所以f(x)在(﹣∞,a)上单调递减.
综上所述,f(x)在(a,+∞)上单调递增,在(﹣∞,a)上单调递减
(3)解:g(x)=  .
.
∵y1=x2+(2﹣2a)x的对称轴为x=a﹣1,y2=x2﹣2ax+2a的对称轴为x=a,y3=x2﹣(2a+2)x+2a的对称轴为x=a+1,
∴g(x)在(﹣∞,0)上单调递减,在(0,a)上单调递减,在(a,+∞)上单调递增.
∵g(0)=2a>0,g(a)=a2+(2﹣2a)a=2a﹣a2=﹣(a﹣1)2+1,
∵a>2,∴g(a)=﹣(a﹣1)2+1在(2,+∞)上单调递减,
∴g(a)<g(2)=0.
∴f(x)在(0,a)和(a,+∞)上各有一个零点.
综上所述,当a>2时,g(x)=f(x)+|x|有两个零点
【解析】(1)根据f(0)≤1列不等式,对a进行讨论解出a的范围;(2)根据二次函数的对称轴和开口方向判断单调区间;(3)写出g(x)的函数解析式,利用二次函数的性质判断g(x)的单调性,根据零点的存在性定理判断.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2-e2x.
(1)若曲线y=f(x)在点(2,f(2))处的切线平行于x轴,求函数f(x)的单调区间;
(2)若x>0时,总有f(x)>-e2x,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)满足:对任意x∈R,都有f(x+1)+f(x)=2x2﹣2x﹣3
(1)求f(x)的解析式;
(2)若关于x的方程f(x)=a有两个实数根x1 , x2 , 且满足:﹣1<x1<2<x2 , 求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
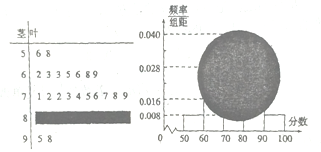
(1)求全班人数及分数在![]() 之间的频数;
之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中![]() 间的矩形的高;
间的矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,又数列{ ![]() }(n∈N*)是公差为1的等差数列.
}(n∈N*)是公差为1的等差数列.
(1)求数列{an}的通项公式an;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设倾斜角为α的直线: ![]() (t为参数)与曲线C:
(t为参数)与曲线C: ![]() (θ为参数)相交于不同的两点A,B.
(θ为参数)相交于不同的两点A,B.
(1)若α= ![]() ,求线段AB的长度;
,求线段AB的长度;
(2)若直线的斜率为 ![]() ,且有已知点P(2,
,且有已知点P(2, ![]() ),求证:|PA||PB|=|OP|2 .
),求证:|PA||PB|=|OP|2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com