
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
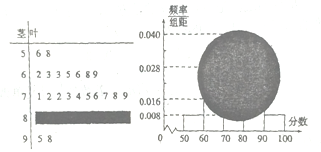
(1)求全班人数及分数在![]() 之间的频数;
之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中![]() 间的矩形的高;
间的矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在
之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在![]() 之间的概率.
之间的概率.
【答案】(1)全班人数为25;分数在![]() 之间的频数为4
之间的频数为4
(2)该班的平均分数为74;频率分布直方图中![]() 间的矩形的高为0.016;
间的矩形的高为0.016;
(3)![]()
【解析】试题分析:(1)由频率分布直方图可知分数在[50,60)的频率为0.008×10=0.08,再由茎叶图知分数在[50,60)之间的频数为2,则全班人数为![]() ;(2)[80,90)之间的人数为
;(2)[80,90)之间的人数为![]() 人,根据对应的频率为
人,根据对应的频率为![]() ,所以矩形的高为
,所以矩形的高为![]() ;(3)根据列举法能够知道在[80,100]之间的试卷中任取两份的基本事件15个,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是
;(3)根据列举法能够知道在[80,100]之间的试卷中任取两份的基本事件15个,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是![]() .
.
试题解析:(1)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知:分数在[50,60)之间的频数为2,
所以全班人数为![]() .
.
(2)由(1)知,分数在[80,90)之间的人数为![]() 人. 则对应的频率为
人. 则对应的频率为![]() ,所以[80,90)间的矩形的高为
,所以[80,90)间的矩形的高为![]() .
.
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,在[80,100]之间的试卷中任取两份的基本事件为:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.其中,至少有一个在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 为正方形,
为正方形, ![]() 为直角梯形,
为直角梯形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() .
.
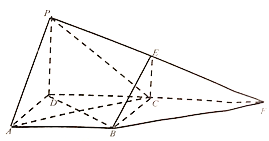
(1)若![]() 和
和![]() 延长交于点
延长交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 边上的动点,求直线
边上的动点,求直线![]() 与平面
与平面![]() 所成角正弦值的最小值.
所成角正弦值的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》,自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求“幼儿园、中小学等教育机构停课,停课不停学”学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的,某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |

(1)请在图中完成被调查人员年龄的频率分布直方图;
(2)若从年龄在![]() ,
, ![]() 两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为
两组采访对象中各随机选取2人进行深度跟踪调查,选中4人中不赞成这项举措的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=(x﹣a)2+|x﹣a|﹣a(a﹣1).
(1)若f(0)≤1,求a的取值范围;
(2)求f(x)在R上的单调区间(无需使用定义严格证明,但必须有一定的推理过程);
(3)当a>2时,求函数g(x)=f(x)+|x|在R上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:f(x)=2 ![]() cos2x+sin2x﹣
cos2x+sin2x﹣ ![]() +1(x∈R).求:
+1(x∈R).求:
(1)f(x)的最小正周期;
(2)f(x)的单调增区间;
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣8≤0},B={x| ![]() <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间 ![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某影院为了宣传影片《战狼Ⅱ》,准备采用以下几种方式来扩大影响,吸引市民到影院观看影片,根据以往经验,预测:
①分发宣传单需要费用1.5万元,可吸引30%的市民,增加收入4万元;
②网络上宣传,需要费用8千元,可吸引20%的市民,增加收入3万元;
③制作小视频上传微信群,需要费用2.5万元,可吸引35%的市民,增加收入5.5万元;
④与商场合作需要费用1万元,购物满800元者可免费观看影片(商场购票),可吸收15%的市民,增加收入2.5万元,
问: (1)在三个观看影片的市民中,至少有一个是通过微信群宣传方式吸引来的概率是多少?
(2)影院预计可增加盈利是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com