
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 24 |
| 3 |
| 4 |
| 3 |
| π |
| 6 |
| 5 |
| 24 |
| 3 |
| 4 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5 |
| 24 |
| 3 |
| 4 |
| π |
| 6 |
| π |
| 4 |
| 4π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 4π |
| 3 |
| 3π |
| 4 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |


科目:高中数学 来源: 题型:
 如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=
如图,矩形ABCD所在的平面与平面ABF互相垂直,在△ABF中,AB=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 2an |
| (an-2)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| -x2-4x+5 |
| 2x|x-a| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90] | 4 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
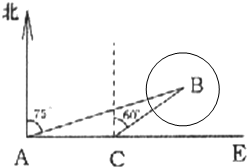 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.
如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com