Question

15．如图，D是△ABC外接圆上的一点，弦AD与BC交于点E，且AB=AC=6，AE=4．
（Ⅰ）求线段DE的长；
（Ⅱ）若∠BAC=120°，求△BCD内切圆的面积．

Answer 1

分析 （Ⅰ）连接BD构造相似三角形△ABE∽△ADB，然后根据相似三角形的对应边成比例求得AB²=AD•AE，从而求得AB的长度．
（Ⅱ）利用三角形相似求出三角形的三个边长，通过三角形的面积求出内切圆的半径，然后求解内切圆的面积．

解答 解：（Ⅰ）如图，AB=AC=6，
则$\widehat{AB}=\widehat{AC}$，
∴∠ABE=∠D（等弧所对的圆周角相等），
又∠BAE=∠BAD（公共角），
∴△ABE∽△ADB（AA），
∴$\frac{AB}{AD}=\frac{AE}{AB}$（相似三角形的对应边成比例），
∴AB²=AD•AE=（AE+ED）•AE，又AE=4，AB=6，得ED=5．
（Ⅱ）∠BAC=120°，BC=6$\sqrt{3}$，BE=3$\sqrt{3}+$$\sqrt{7}$，EC=3$\sqrt{3}-\sqrt{7}$，CD=$\frac{ED•AB}{BE}$=$\frac{5×6}{3\sqrt{3}+\sqrt{7}}$=$\frac{9\sqrt{3}-3\sqrt{7}}{2}$，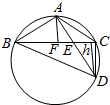
△DBE∽△AEC，∴$\frac{BE}{BD}=\frac{AE}{AC}$，可得BD=$\frac{AC•BE}{AE}$=$\frac{9\sqrt{3}+3\sqrt{7}}{2}$．D到BC的距离为h，则$\frac{AE}{AF}=\frac{DE}{h}$，h=$\frac{15}{4}$，$\frac{1}{2}BC•h=\frac{1}{2}（BC+BD+DC）•r$，（r是△BCD内切圆的半径），
$\frac{1}{2}$×$6\sqrt{3}×\frac{15}{4}$=$\frac{1}{2}$×（$6\sqrt{3}+\frac{9\sqrt{3}+3\sqrt{7}}{2}+\frac{9\sqrt{3}-3\sqrt{7}}{2}$）•r，解得r=$\frac{3}{2}$，
△BCD内切圆的面积：$（\frac{3}{2}）^{2}π$=$\frac{9π}{4}$．

点评 本题综合考查了相似三角形的判定与性质、圆周角定理．圆心角与它所对的弧、所对的弦之间的关系：这三个量中，若有一个量相等，则其它的量两个量也相等．考查内切圆的面积的求法，考查转化思想的应用．