
在边长为a的正方形ABCD所在平面外取一点P,使PA⊥平面ABCD,且PA=AB,在AC的延长线上取一点G。
(1)若CG=AC,求异面直线PG与CD所成角的大小;
(2)若CG=AC,求点C到平面PBG的距离;
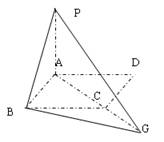
(3)当点G在AC的延长线上运动时(不含端点C),求二面角P-BG-C的取值范围。
(1)![]() (2)
(2)![]() (3)二面角P-BG-C的取值范围是
(3)二面角P-BG-C的取值范围是![]()
分析:本题如利用“几何法”,则通过“平移变换”将异面直线角化归为三角形的内角,由解三角形的方法求之,凡“点面距离”可利用等积法求之,至于二面角,则通过“作-证-算”三步曲求得;本题如利用“向量法”,则建立适当的空间直角坐标系,写出各点坐标,再根据公式而求之。
方法一:(1)过点G作GE∥CD交AD的延长线于点E,连PE,则∠PGE是异面直线PG与CD所成的角,,则由条件得GE=2a,PG=3a,
cos ∠PGE=![]() ,所以异面直线PG与CD所成角等于
,所以异面直线PG与CD所成角等于![]() ;
;
(2)设h,则利用等积法知![]() ,在△PBG中,PB=
,在△PBG中,PB=![]() ,PG=3a,BG=
,PG=3a,BG=![]() ,
,![]() ,得
,得![]() ,又在△CBG中,
,又在△CBG中,![]() ,从而由
,从而由![]() 得
得![]() ;
;
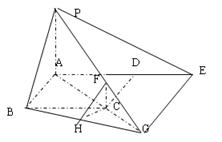
(3)作CF⊥AC交PG于F,作FH⊥BG交BG于H,连CH,因为PA⊥平面ABCD,所以PA⊥AC,所以PA∥CG,得CG⊥平面ABCD,由三垂线定理得∠FHC是二面角P-BG-C的平面角,设![]() ,则由△CGF∽△AGP得
,则由△CGF∽△AGP得![]() ,
,
在△CBG中![]() ,得
,得![]()
所以![]() ,从而
,从而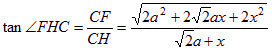
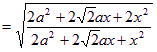
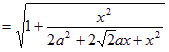
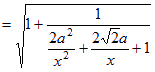
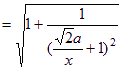
![]() ,所以二面角P-BG-C的取值范围是
,所以二面角P-BG-C的取值范围是![]() 。
。
方法二:建立如图所示的直角坐标系,
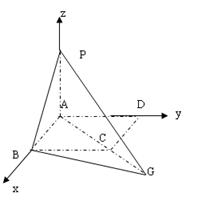
则A(0,0,O、0),B(a,0,0),C(a,a,0),D(0,a,0),P(0,0,a)。
由条件得G(2 a ,2 a ,0),
![]() ,
,![]()
所以![]() ,
,
所以异面直线PG与CD所成角等于![]() ;
;
(2)设平面PBG的法向量为![]() 因
因![]() ,
,![]()
所以由![]() 得
得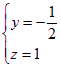 ,即
,即![]() 又
又![]() ,
,
所以点C到平面PBG的距离为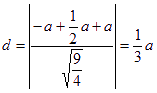 ;
;
由条件设G(t,t,0), 其中![]() ,平面PBG的法向量为
,平面PBG的法向量为![]()
因![]() ,
,![]() ,所以由
,所以由![]() 得
得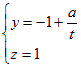 ,
,
即![]() 而平面CBG的法向量
而平面CBG的法向量![]() ,
,
所以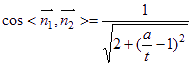 ,因为
,因为![]() ,所以
,所以![]() ,
,
易知二面角P-BG-C的平面角是锐角,所以二面角P-BG-C的平面角等于![]() ,所以二面角PP-BG-C的取值范围是
,所以二面角PP-BG-C的取值范围是![]() 。
。
点评:本题主要考查异面直线所成角的空间想象能力,利用体积法求点面距离的运算能力,二面角的估算能力,第(3)问有机的将函数的值域与立体几何结合,较好地考查学生综合分析与解决问题的能力.


科目:高中数学 来源: 题型:
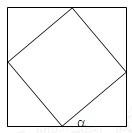 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为
如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
(2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第92-93课时):第十二章 极限-数列的极限、数学归纳法(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com