
【题目】美国制裁中兴,未来7年一颗芯片都不卖,这却激发了中国“芯”的研究热潮.某公司甲,乙,丙三个研发小组分别研发![]() ,
,![]() ,
,![]() 三种不同的芯片,现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析,有关数据见下表(单位:件).
三种不同的芯片,现在用分层抽样的方法从这些芯片中抽取若干件进行质量分析,有关数据见下表(单位:件).
芯片 | 数量 | 抽取件数 |
| 200 |
|
| 600 |
|
| 400 | 2 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若在这抽出的样品中随机抽取2件送往某机构进行进一步检测,求这2件芯片来自不同种类的概率.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流![]() 类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:
类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)将同一组数据用该区间的中点值作代表,求这100人月薪收入的样本平均数![]() ;
;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间![]() 右侧的每人收取800元;
右侧的每人收取800元;
方案二:每人按月薪收入的样本平均数的![]() 收取;
收取;
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的左焦点为
,椭圆的左焦点为![]() ,椭圆上任意点到
,椭圆上任意点到![]() 的最远距离是
的最远距离是![]() ,过直线
,过直线![]() 与
与![]() 轴的交点
轴的交点![]() 任作一条斜率不为零的直线
任作一条斜率不为零的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .
.
(1)求椭圆的方程;
(2)求证:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数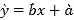 ,回归直线方程
,回归直线方程![]() ,
,
其中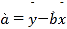 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com