
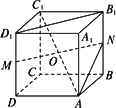
如图,在正方体A1B1C1D1-ABCD中,棱长为a,求两异面直线B1D1和C1A所成的角.
|
解法1:取D1D、B1B的中点分别为M、N,连结MN,则B1D1∥MN,且MN过正方体的中心O点,又由点O∈C1A,连结AN,则∠AON为所求异面直线B1D1和C1A所成的角或其补角. ∵B ∵正方体棱长为a, ∴MN=B1D1= 又∵O是正方体对称中心,∴ON= ∴AO2+ON2=( ∴△AON是直角三角形, 即∠AON=90°.故异面直线B1D1和C1A所成角是90°. 解法2:(补体法)在原正方体A1B1C1D1-ABCD的旁边,补上一个与原正方体棱长相等的正方体,如图所示.取新正方体与A1D1在同一直线的顶点为E,连结C1E、AE,由正方体性质可知,C1E
∴∠EC1A为所求两异面直线B1D1和C1A所成的角或其补角. ∵正方体棱长为a,由正方体性质知C1E= 又EA2=A1A2+AE2=a2+(2a)2=5a2=C1E2+C1A2, ∴△EAC1是直角三角形,∠EC1A=90°. 深化升华:割补法在立体几何中有广泛的用途,对于“补”来说,可以全补(如本例)也可以“局部补形”(如本例只将底面A1B1C1D1延伸至A1B1E,所作平行线为EC1,构成△EAC1),都可以达到目的. |
|
可将B1D1平移,使B1移到C1或A1;也可将C1A平移,使C1移到B1或D1,但此时B1D1落到正方体外面去了或C1A落到正方体外面去了,给解题带来了困难,如果利用正方体的对称中心,也能求出异面直线所成的角. |


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
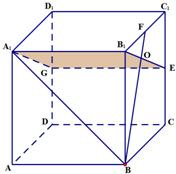 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别为CC1、B1C1、DD1的中点,O为BF与B1E的交点,
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别为CC1、B1C1、DD1的中点,O为BF与B1E的交点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com