分析:(1)先在正方形BCC1B1中根据条件得到△BB1F≌△B1C1E,进而推得 BF⊥B1E;再结合DC⊥平面BCC1B1,GE∥DC得到BF⊥GE即可证明结论;
(2)由(1)知,BO⊥平面A1B1EG;得到∠BA1O即为直线A1B与平面A1B1EG所成角;然后通过求边长即可求出结论.
解答: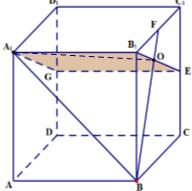
(1)证明:因为 BB
1=B
1C
1,B
1F=C
1E,BF=B
1E
所以△BB
1F≌△B
1C
1E
从而∠C
1EB
1=∠BFB
1在Rt△B
1C
1E中∠C
1EB
1+∠C
1B
1E=90°
故∠BFB
1+∠C
1B
1E=90°从而∠FOB
1=90°
即BF⊥B
1E…(2分)
又因为DC⊥平面BCC
1B
1,GE∥DC
所以GE⊥平面BCC
1B
1…(4分)
又因为BF?平面BCC
1B
1故BF⊥GE
又因为B
1E∩GE=E
所以BF⊥平面A
1B
1EG…(6分)
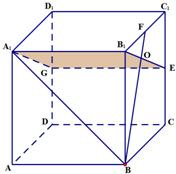
(2)解:如右图,连接A
1O
由(1)知,BO⊥平面A
1B
1EG
故∠BA
1O即为直线A
1B与平面A
1B
1EG所成角…(8分)
设正方体的棱长为1,则
A1B=,
BF==在Rt△BB
1F中,有
=故
BO==
=
…(10分)
所以
sin∠BA1O===…(12分)
点评:本题主要考查线面垂直的判定以及直线和平面所成的角的求法.在证明线面垂直时,一般时先证明线线垂直,即证直线和平面内的两条相交直线垂直,从而得到线面垂直.

 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别为CC1、B1C1、DD1的中点,O为BF与B1E的交点,
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别为CC1、B1C1、DD1的中点,O为BF与B1E的交点, (1)证明:因为 BB1=B1C1,B1F=C1E,BF=B1E
(1)证明:因为 BB1=B1C1,B1F=C1E,BF=B1E

 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则