练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．在空间直角坐标系中，已知点A（2，4，-3），B（0，6，-1），则以线段AB为直径的圆的面积等于3π．

    分析 利用两点间距离公式先求出|AB|，从而求出圆半径，进而求出圆面积．

    解答 解：∵点A（2，4，-3），B（0，6，-1），
    ∴|AB|=$\sqrt{{{（2-0）}^2}+{{（4-6）}^2}+{{（-3-（-1））}^2}}=2\sqrt{3}$，
    ∴以线段AB为直径的圆的半径为$\sqrt{3}$，
    面积等于$S={（\sqrt{3}）^2}π=3π$．
    故答案为：3π．

    点评 本题考查圆的面积的求法，是基础题，解题时要认真审题，注意两点间距离公式的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

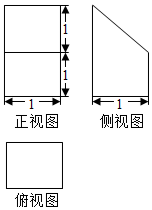    12．某几何体的三视图如图所示，则该几何体的表面积等于（　　）
    A．7+$\sqrt{2}$B．6+$\sqrt{2}$C．$\frac{3}{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．如图所示，小华单位的圆柱形注水罐的底面半径为2m、高为3m，若每小时灌入该注水罐的水的体积为3m3，则经过多少小时该注水罐灌满？（注意：π取近似值3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知$\overrightarrow{a}$⊥$\overrightarrow{b}$，并且$\overrightarrow{a}$=（3，x），$\overrightarrow{b}$=（7，12），则x=（　　）
    A．-$\frac{7}{4}$B．$\frac{7}{4}$C．-$\frac{7}{3}$D．$\frac{7}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．从某大学一年级女生中，选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名，其身高和体重数据如表所示：
    身高/cm（x）150155160165170
    体重/kg（y）4346495156
    （1）求y关于x的线性回归方程；
    （2）利用（1）中的回归方程，计算身高为168cm时，体重的估计值$\stackrel{∧}{y}$为多少？
        参考公式：线性回归方程 $\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设f（x）=e2x，若函数g（x）的图象与函数f（x）的图象关于直线y=x对称，则g（x）=（　　）
    A．2lnxB．$\frac{1}{2}$lnxC．ln（2x）D．ln（$\frac{1}{2}$x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．某产品的广告费用x与销售额y的统计数据如表：
    广告费用x（万元）3456
    销售额y（万元）25304045
    根据上表可得回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=7，则$\stackrel{∧}{a}$=3.5，据此模型预报广告费为7万元时销售额为52.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知函数f（x）=x3+ax2+bx+c，给出四个结论：
    ①函数f（x）一定有两个极值点．
    ②若x=x0是f（x）的极小值点，则f（x）在区间（-∞，x0）上单调递减．
    ③f（x）的图象是中心对称图形．
    ④若f′（x0）=0，则x=x0是f（x）的极值点．
    则结论正确的有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在△ABC中，∠A=60°，AB=2，且△ABC的面积S=$\frac{\sqrt{3}}{2}$，则AC的长为（　　）
    A．2B．1C．$\sqrt{3}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    同步练习册答案