
| A. | 6 | B. | $6+\sqrt{2}$ | C. | 8 | D. | $4+2\sqrt{2}$ |
分析 由对数的运算性质可得x+2y=1,即有$\frac{2}{x}+\frac{1}{y}$=(x+2y)($\frac{2}{x}$+$\frac{1}{y}$)=4+$\frac{x}{y}$+$\frac{4y}{x}$,运用基本不等式即可得到最小值.
解答 解:ln3x+ln9y=ln3可得,
3x•9y=3,
即为3x+2y=3,
即有x+2y=1,
则$\frac{2}{x}+\frac{1}{y}$=(x+2y)($\frac{2}{x}$+$\frac{1}{y}$)=4+$\frac{x}{y}$+$\frac{4y}{x}$≥4+2$\sqrt{\frac{x}{y}•\frac{4y}{x}}$=8,
当且仅当x=2y=$\frac{1}{2}$时,取得最小值8.
故选C.
点评 本题考查运用基本不等式求最值的方法,考查乘1法和对数函数的运算性质,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
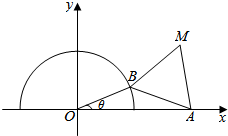 如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.
如图,已知半圆O:x2+y2=1(y≥0)及点A(2,0),B为半圆周上任意一点,以AB为一边作等边△ABM.设∠AOB=θ,其中0<θ<π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
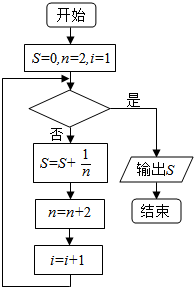 如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )
如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{96}$的值的一个程序框图,其中判断框内应填入的条件是( )| A. | i>48 | B. | i>24 | C. | i<48 | D. | i<24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过,其中AD=$\sqrt{2}$,DC=2,BC=1,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是1-$\frac{π}{10}$.
一只受伤的丹顶鹤在如图所示(直角梯形)的草原上飞过,其中AD=$\sqrt{2}$,DC=2,BC=1,它可能随机在草原上任何一处(点),若落在扇形沼泽区域ADE以外丹顶鹤能生还,则该丹顶鹤生还的概率是1-$\frac{π}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com