


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
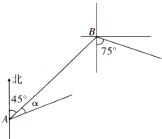 在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)
在一次海上联合作战演习中,红方一艘侦察艇发现在北偏东45°方向,相距12n mile的水面上,有蓝方一艘小艇正以每小时10n mile的速度沿南偏东75°方向前进,若侦察艇以每小时14n mile的速度,沿北偏东45°+α方向拦截蓝方的小艇,若要在最短的时间内拦截住,求红方侦察艇所需的时间和角α的正弦值.(注:n mile是海里的英文符号)查看答案和解析>>
科目:高中数学 来源: 题型:
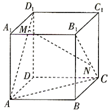 如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是
如图,棱长为2的正方体ABCD-A1B1C1D1中,M,N分别是线段AD1和B1C上的动点,且满足D1M=CN,则下列命题正确的是查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com