练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

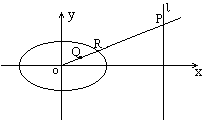
    已知椭圆，直线l：x=12，P是l上一点，射线OP交椭圆于点R，又点Q在OP上，且满足|OQ|·|OP|=|OR|2，当点P在l上移动时，求点Q的轨迹方程，并说明轨迹是什么曲线．

     

    答案：
    解析：

    		解：设点P、Q、R的坐标分别为(12，yp)，(x，y)，

    (xR，yR )题设知xR>0，x>0，

    由点R在椭圆上及点O、Q、R共线，得方程组

        解得       ①

                      ②

    由点O、Q、P共线，得，即yp=．       ③

    由题设|OQ|·|OP|=|OR|2得

    将①、②、③式代入上式，整理得点Q的轨迹方程

    (x－1)2+=1           (x>0)

    所以点Q的轨迹是以(1，0)为中心，长、短半轴长分别为1和，

    且长轴在x轴上的椭圆、去掉坐标圆点．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黑龙江省哈三中2011－2012学年高二上学期期中考试数学理科试题 题型：044

    已知椭圆和直线l：x＋2y＋m＝0

    (Ⅰ)当m＝4时，若点P是椭圆上一点，求点P到直线l距离的最大值；

    (Ⅱ)当m＝－2时，直线l与椭圆交于A、B两点，求|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知椭圆数学公式及直线l：y=x+m．
    （1）当直线l与椭圆有公共点时，求实数m的取值范围；
    （2）若直线l过椭圆右焦点，并与椭圆交于A、B两点，求弦AB之长．

    查看答案和解析>>

    科目：高中数学 来源：湖南省期中题 题型：解答题

    已知椭圆及直线l：y=x+m。
    （1）当直线l与椭圆有公共点时，求实数m的取值范围；
    （2）求直线l被椭圆截得的弦长的最大值。

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年福建省泉州市南安一中高二（上）年期末数学试卷（文科）（解析版） 题型：解答题

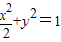    已知椭圆及直线l：y=x+m．
    （1）当直线l与椭圆有公共点时，求实数m的取值范围；
    （2）若直线l过椭圆右焦点，并与椭圆交于A、B两点，求弦AB之长．

    查看答案和解析>>

    同步练习册答案