

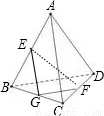
 解:取BC的中点G,连接EG,FG,
解:取BC的中点G,连接EG,FG,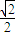
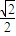


科目:高中数学 来源: 题型:
 如图,正四面体ABCD的棱长均为a,且AD⊥平面α于A,点B、C、D均在平面α外,且在平面α同一侧,则点B到平面α的距离是( )
如图,正四面体ABCD的棱长均为a,且AD⊥平面α于A,点B、C、D均在平面α外,且在平面α同一侧,则点B到平面α的距离是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•绍兴一模)如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为45°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值等于( )
(2013•绍兴一模)如图,正四面体ABCD的顶点C在平面α内,且直线BC与平面α所成角为45°,顶点B在平面α上的射影为点O,当顶点A与点O的距离最大时,直线CD与平面α所成角的正弦值等于( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正四面体ABCD中,E在棱AB上,F在棱CD上,使得
如图,正四面体ABCD中,E在棱AB上,F在棱CD上,使得| AE |
| EB |
| CF |
| FD |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年大连市一模理) 如图,正四面体A―BCD的棱长为a,点E、F分别是棱BD、BC的中点,则平面AEF截该正四面体的内切球所得截面的面积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com