
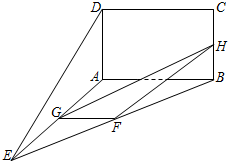
 (2011•宁德模拟)如图,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点.
(2011•宁德模拟)如图,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点.| π | 4 |

| 3 |
| 3 |
| 3 |
| GF |
| BD |
| BG |
| 3 |
| GP |
| GF |
| BP |
| BG |
| GP |
| 3 |
| n |
|
|
| 3 |
| 3 |
| n |
| 3 |
| 3 |
| n |
| n |
| n |
n1•
| ||||
|
|
2
| ||
|
| ||
| 2 |
| GP |
| GF |
| GP |
| GF |
| 3 |
| 3 |


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com