
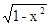 =k(x-2)+1有两解则k的取值范围是
=k(x-2)+1有两解则k的取值范围是  名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
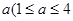 ,且
,且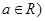 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度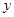 (克/升)随着时间
(克/升)随着时间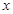 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为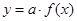 ,其中
,其中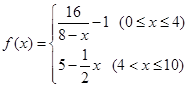 .
.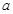 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求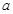 的最小值.(精确到0.1,参考数据:
的最小值.(精确到0.1,参考数据: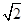 取1.4)
取1.4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com