
 在
在 内有解,则
内有解,则 的图象是( )
的图象是( )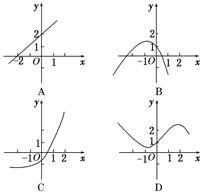
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由. )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其中e是自然数的底数,
,其中e是自然数的底数, 。
。 时,解不等式
时,解不等式 ;
; 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求 的取值范围;
的取值范围; 时,求整数k的所有值,使方程
时,求整数k的所有值,使方程 在[k,k+1]上有解。
在[k,k+1]上有解。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系式可近似的表示为:
(吨)之间的函数关系式可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
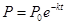 .若在前5个小时消除了
.若在前5个小时消除了 的污染物,则污染物减少
的污染物,则污染物减少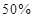 所需要的时间约为( )小时. (已知lg2=0.3010,lg3=0.4771)
所需要的时间约为( )小时. (已知lg2=0.3010,lg3=0.4771)| A.26 | B.33 | C.36 | D.42 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com