分析:(1)t=
时,求出函数y的定义域M,判定f(x)在M上的单调性与最值情况,求出结果;
(2)利用导函数判定函数g(x)在M上的单调性,求出|g(x
1)-g(x
2)|的表达式,根据题中条件求出t的取值范围.
解答:解:(1)t=
时,函数y=lg(1+tx-x
2)的定义域为
1+ x-x2>0,解得
-<x<2,即
M=(-, 2).
∵f(x)=3•4
x-2
x+2=3•(2
x)
2-4•2
x,
令2
x=t,则
<t<4,
f(x)=g(t)=3t2-4t=3(t-)2+,
∴g(t)在
(, 4)上是增函数.
∴g(t)在
(, 4)上无最小值,即f(x)在M上无最小值.
(2)∵函数g(x)=
,∴
g′(x)=>0,
∴g(x)在M上是增函数;
设1+tx-x
2=0的两根为α,β(α<β),则α+β=t,αβ=-1,M=(α,β);
∴
g(β)-g(α)=-=
| (2β-t)(α2+1)-(2α-t)(β2+1) |
| (α2+1)(β2+1) |
=
| 2αβ(α-β)-2(α-β)-t(α-β)(α+β) |
| (αβ)2+(α+β)2-2αβ+1 |
=
=β-α
=
=
.
由题意知,要使原不等式恒成立,只需
<3,
解得
t∈[-, ];
∴t的取值范围是[-
,
].
点评:本题考查了复合函数的定义域与值域、单调性等综合性知识,是容易出错的题目.



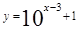 (x≥3)
(B)
(x≥3)
(B) 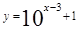 (x∈R)
(x∈R)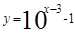 (x∈R) (D)
(x∈R) (D) 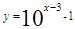 (x≥3)
(x≥3)