【答案】
分析:(Ⅰ)由f(x)=(x
2-3x+3)e
x,x∈[-2,t](t>-2),知f′(x)=(2x-3)e
x+e
x(x
2-3x+3)=e
xx(x-1).由此能求出当t<1时,函数y=f(x)的单调区间.
(Ⅱ)令m=f(-2)=13e
-2,n=f(t)=(t
2-3t+3)e
t,设h(t)=n-m=(t
2-3t+3)e
t-13e
-2,故h′(t)(2t-3)e
t+e
t(t
2-3t+3)=e
t(t
2-3t+3),列表讨论知h(t)的极小值为h(1)=e->0,由此能够证明n>m.
(Ⅲ)由g(x)=(x
2-3x+3)e
x+(x-2)e
x=(x
2-2x+1)e
x=(x-1)2 e
x,知g′(x)=(2x-2)e
x+e
x(x
2-2x+1)=e
x(x
2-1),设x>1时,假设存在[a,b],使y=g(x)在[a,b]上的值域也是[a,b].由此能够推导出不存在区间[a,b]满足题意.
解答:解:(Ⅰ)∵f(x)=(x
2-3x+3)e
x,x∈[-2,t](t>-2),
∴f′(x)=(2x-3)e
x+e
x(x
2-3x+3)=e
xx(x-1).
①当-2<t≤0时,x∈(-2,t),f′(x)>0,f(x)单调递增.
②当0<t<1时,x∈(-2,0),f′(x)>0,f(x)单调递增.
x∈(0,t),f′(x)<0,f(x)单调递减.
综上所述,当-2<t≤0时,y=f(x)单调递增区间为(-2,t);
当0<t<1时,y=f(x)单调递增区间为(-2,0),减区间为(0,t).
(Ⅱ)f(t)>f(-2).
证明:令m=f(-2),n=f(t),则m=13e
-2,n=(t
2-3t+3)e
t,
设h(t)=n-m=(t
2-3t+3)e
t-13e
-2,
∴h′(t)=(2t-3)e
t+e
t(t
2-3t+3)
=e
tt(t-1),(t>-2).
h(t),h′(t)随t变化如下表:

由上表知h(t)的极小值为h(1)=e-

=
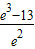
>0.
又h(-2)=0,
∴当t>-2时,h(t)>h(-2)>0,即h(t)>0.
因此,n-m>0,即n>m,
所以f(t)>f(-2).
(Ⅲ)g(x)=(x
2-3x+3)e
x+(x-2)e
x=(x
2-2x+1)e
x=(x-1)2 e
x,
g′(x)=(2x-2)e
x+e
x(x
2-2x+1)=e
x(x
2-1),
设x>1时,g(x)存在保值区间,即存在[a,b],使y=g(x)在[a,b]上的值域也是[a,b].
因为x>1时,g′(x)>0,所以y=g(x)单调递增.
故应有

,
即方程(x-1)
2e
x=x有两个大于1的不等根,
设φ(x)=(x-1)
2e
x-x,(x>1),
φ′(x)=e
x(x
2-1)-1,
设k(x)=e
x(x
2-1)-1,(x>1),k′(x)=e
x(x
2+2x-1),
当x>1时,k′(x)>0,即k(x)在(1,+∞)递增,
又k(1)=-1<0,k(2)=3e
2-1>0.
∴x∈(1,2)时存在唯一的x
,使k(x
)=0.
即存在唯一的x
,使φ′(x
)=0.
φ(x),φ′(x)随x的变化如下表:

由上表知,φ(x
)<φ(1)=-1<0,
φ(2)=e
2-2>0,
故y=φ(x)的大致图象如图,

因此φ(x)在(1,+∞)只能有一个零点,
这与φ(x)=0有两个大于1的不等根矛盾,
故不存在区间[a,b]满足题意,即函数g(x)不存在保值区间.
点评:本题考查函数的单调区间的求法,考查不等式的证明,探索满足条件的区间是否存在.综合性强,难度大,具有一定的探索性,对数学思维的要求较高,解题时要认真审题,仔细解答,注意导数性质的灵活运用


 =
=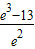 >0.
>0. ,
,



 备战中考寒假系列答案
备战中考寒假系列答案