
| A. | ① | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 画出函数的图象,以及根据m,n的几何意义即可判断.
解答 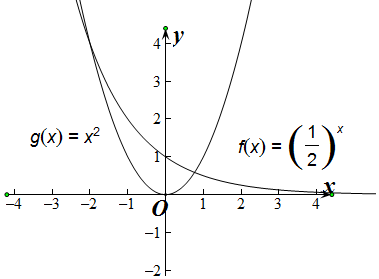 解:分别画出函数f(x),g(x)的图象,
解:分别画出函数f(x),g(x)的图象,
则m=$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}$表示曲线f(x)上两点的斜率,n=$\frac{{g({x_1})-g({x_2})}}{{{x_1}-{x_2}}}$表示曲线g(x)上两点的斜率,
由图象可知,①对于任意不相等的实数x1,x2,都有m<0,故①正确,
对于任意不相等的实数x1,x2,都有n>0或n<0,故②错误,
存在不相等的实数x1,x2,使得m=n,故③正确,
故选:B
点评 本题考查了函数图象的画法和函数图象的几何意义,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com