
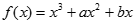 在
在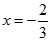 与
与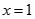 处都取得极值.
处都取得极值.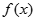 的解析式;
的解析式;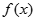 在区间[-2,2]的最大值与最小值.
在区间[-2,2]的最大值与最小值.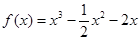 ;(2)
;(2)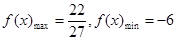 .
.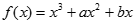 在
在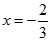 与
与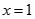 处都取得极值,得到
处都取得极值,得到 ,求出
,求出 得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数
得到:关于a,b的两个方程,联立解方程组可得到a,b的值,从而可写出函数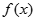 的解析式;(2)由(1)已求出
的解析式;(2)由(1)已求出 的解析式,要求函数
的解析式,要求函数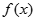 在区间[-2,2]的最大值与最小值,只需先求出函数
在区间[-2,2]的最大值与最小值,只需先求出函数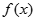 在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值.
在区间[-2,2]的极大值与极小值,再求出两个端点的函数值,然后比较这四个数值的大小,得其中的最大者就是该函数的最大值,最小者就是该函数的最小值. )=
)= ,f¢(1)=3+2a+b=0 3分
,f¢(1)=3+2a+b=0 3分 ,b=-2 5分
,b=-2 5分 ,b=-2符合题意
,b=-2符合题意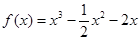 6分
6分 | x | (-2,-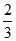 ) ) | -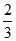 | (-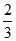 ,1) ,1) | 1 | (1,2) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |
 11分
11分  时,
时, 12分
12分

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
 (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R ,需用白铁皮的面积记为
,需用白铁皮的面积记为 (不计接头等)。
(不计接头等)。 表示为R的函数;
表示为R的函数; 的最小值及对应的粮囤的总高度。(含圆锥顶盖)
的最小值及对应的粮囤的总高度。(含圆锥顶盖)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com