Question

若三棱锥A—BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等，则动点P的轨迹与△ABC组成的图形可能是（    ）

Answer 1

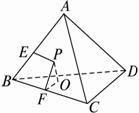
解法一：如图，PO为P到平面BCD的距离，PE为P到棱的距离.过P作PF⊥BC于F,连结OF,则∠PFO为侧面ABC与底面BCD所成二面角的平面角.

    设∠PFO=θ,则sinθ=.

    又PO=PE,

∴sinθ=,即在侧面ABC内P点到边AB、BC的距离之比为sinθ.故P点的轨迹是直线段.

解法二:如下图,在AC上一定存在一点使得到平面BCD的距离和它到AB的距离相等,假设为E点,则EO⊥平面BCD于O,EF⊥AB于F,且EF=EO,连结BE,则BE即为所求.

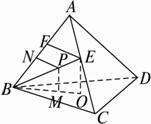
证明:∵EF=EO,BE=BE,

∴Rt△EFB≌Rt△EOB.

∴∠EBF=∠EBO.

    设P为BE上任一点,PN⊥AB,PM⊥平面BCD,M、N为垂足，M必在BO上，易证Rt△PNB≌Rt△PMO，

∴PN=PM.

答案：D