
【题目】某校举行运动会,其中三级跳远的成绩在8.0米(四舍五入,精确到0.1米)以上的进入决赛,把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
(Ⅰ)求进入决赛的人数;
(Ⅱ)若从该校学生(人数很多)中随机抽取两名,记X表示两人中进入决赛的人数,求X的分布列及数学期望;
(Ⅲ)经过多次测试后发现,甲成绩均匀分布在8~10米之间,乙成绩均匀分布在9.5~10.5米之间,现甲,乙各跳一次,求甲比乙远的概率.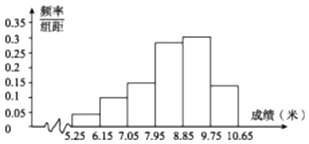
【答案】(Ⅰ)解:第6小组的频率为1﹣(0.04+0.10+0.14+0.28+0.30)=0.14,
∴总人数为 ![]() (人).
(人).
∴第4、5、6组成绩均进入决赛,人数为(0.28+0.30+0.14)×50=36(人)
即进入决赛的人数为36.
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为 ![]() ,
,
∴X~ ![]() ,
, ![]() ,
,
P(X=1)= ![]() ,
,
![]() .
.
∴所求分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
![]() ,两人中进入决赛的人数的数学期望为
,两人中进入决赛的人数的数学期望为 ![]() .
.
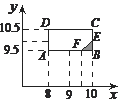
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,
则基本事件满足的区域为: ![]() ,
,
事件A“甲比乙远的概率”满足的区域为x>y,如图所示.
∴由几何概型P(A)= ![]() =
= ![]() .
.
即甲比乙远的概率为 ![]() .
.
【解析】(Ⅰ)由频率分直方图求出第6小组的频率,从而求出总人数,进而得到第4、5、6组成绩均进入决赛,由此能求出进入决赛的人数.
(Ⅱ)由题意知X的可能取值为0,1,2,进入决赛的概率为 ![]() ,从而X~
,从而X~ ![]() ,由此能求出X的分布列及数学期望.
,由此能求出X的分布列及数学期望.
(Ⅲ)设甲、乙各跳一次的成绩分别为x、y米,则基本事件满足的区域为: ![]() ,由此利用几何概型能求出甲比乙远的概率.
,由此利用几何概型能求出甲比乙远的概率.
【考点精析】根据题目的已知条件,利用频率分布直方图的相关知识可以得到问题的答案,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】下列选项中,错误的是( )
A.若p为真,则¬(¬p)也为真
B.若“p∧q为真”,则“p∨q为真”为真命题
C.x∈R,使得tanx=2017
D.“2x> ![]() ”是“log
”是“log ![]() x<0”的充分不必要条件
x<0”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x1 , x2 , x3 , x4},xi∈{﹣1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
A.60
B.65
C.80
D.81
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx.若存在x1 , x2 , ,xm满足0≤x1<x2<<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|++|f(xm﹣1)﹣f(xm)|=12(m≥2,m∈N*),则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣a|,a∈R
(Ⅰ)当a=5,解不等式f(x)≤3;
(Ⅱ)当a=1时,若x∈R,使得不等式f(x﹣1)+f(2x)≤1﹣2m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设函数f(x)=|x+ ![]() |+|x﹣2m|(m>0).
|+|x﹣2m|(m>0).
(Ⅰ)求证:f(x)≥8恒成立;
(Ⅱ)求使得不等式f(1)>10成立的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1的一个焦点为F(2,0),且离心率为
=1的一个焦点为F(2,0),且离心率为 ![]()
(1)求椭圆方程;
(2)过点M(3,0)作直线与椭圆交于A,B两点,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,设椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
=1(a>b>0)的左、右焦点分别为F1 , F2 , 右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.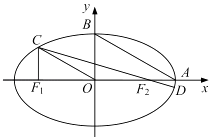
(1)若OC∥AB,求e的值;
(2)连结CF2并延长交椭圆于另一点D若 ![]() ≤e≤
≤e≤ ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com