
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).

某市随机抽取10户同一个月的用电情况,得到统计表如下:

(1)若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯每度0.8元,试计算![]() 居民用电户用电410度时应交电费多少元?
居民用电户用电410度时应交电费多少元?
(2)现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
(3)以表中抽到的10户作为样本估计全市居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.
【答案】(1)![]() 元;(2)分布列见解析,期望为
元;(2)分布列见解析,期望为![]() ;(3)
;(3)![]() .
.
【解析】
(1)将![]() 分成三个部分:
分成三个部分:![]() 元收费的是
元收费的是![]() 度,
度,![]() 元收费的是
元收费的是![]() 度,
度,![]() 元收费的是
元收费的是![]() 度,相加后求得总的费用.(2)由表格数据可知,第二梯度电量用户有
度,相加后求得总的费用.(2)由表格数据可知,第二梯度电量用户有![]() 户,另外
户,另外![]() 户不是,利用超几何分布计算公式,计算出分布列,并求得期望值.(3)由表格数据可知,第一梯度有
户不是,利用超几何分布计算公式,计算出分布列,并求得期望值.(3)由表格数据可知,第一梯度有![]() 户,故概率为
户,故概率为![]() .从全市中依次抽取
.从全市中依次抽取![]() 户,相当于十次独立重复试验,属于二项分布.利用二项分布的概率计算公式,列不等式组,解不等式组求得
户,相当于十次独立重复试验,属于二项分布.利用二项分布的概率计算公式,列不等式组,解不等式组求得![]() 的取值范围.
的取值范围.
(1)![]() 元
元
(2)设取到第二阶梯电量的用户数为![]() ,可知第二阶梯电量的用户有3户,则
,可知第二阶梯电量的用户有3户,则![]() 可取0,1,2,3,
可取0,1,2,3,![]() ,
,![]() ,
,![]() ,
,![]()
故![]() 的分布列为
的分布列为

∴![]()
(3)可知从全市中抽取10户的用电量为第一阶梯,满足![]() ,
,
可知![]() (
(![]() )
)
令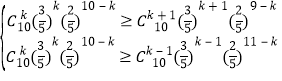
解得:![]() ,
,![]()
∴当![]() 时概率最大,
时概率最大,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知平面四边形MNPQ中,MN=![]() ,MP=1,MP⊥MN,PQ⊥QM.
,MP=1,MP⊥MN,PQ⊥QM.
(Ⅰ)若PQ=![]() ,求NQ的值;
,求NQ的值;
(Ⅱ)若∠MQN=30°,求sin∠QMP的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的焦点,椭圆的右准线
的焦点,椭圆的右准线![]() 与
与![]() 轴交于
轴交于![]() 点,若
点,若![]() ,且
,且![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)过![]() 、
、![]() 作互相垂直的两直线分别与椭圆交于
作互相垂直的两直线分别与椭圆交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=![]() .
.
(1)求直线CD的方程;
(2)求圆P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定一个由![]() 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
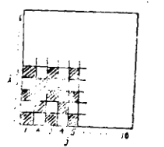
现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里![]() .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
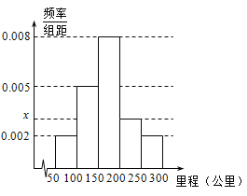
(1)求直方图中![]() 的值;
的值;
(2)求![]() 辆纯电动汽车续驶里程的中位数;
辆纯电动汽车续驶里程的中位数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程为
辆车,求其中恰有一辆车的续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com