
在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为内角
分别为内角![]() 所对的边,且满足
所对的边,且满足![]() .
.![]()
(1)证明:![]() ;
;
(2)如图,点![]() 是
是![]() 外一点,设
外一点,设![]()
![]() ,
,
![]() ,当
,当![]() 时,求平面四边形
时,求平面四边形![]() 面积的最大值.
面积的最大值.
 |
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2013-2014学年安徽“江淮十校”协作体高三上学期第一次联考文数学卷(解析版) 题型:选择题
在 中,已知
中,已知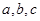 分别为内角
分别为内角 ,
,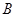 ,
, 所对的边,
所对的边, 为
为 的面积.若向量
的面积.若向量 满足
满足 ,则
,则 ( )
( )
A、 B、
B、 C、
C、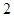 D、
D、
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山西省忻州市高三第一次联考数学文卷 题型:解答题
.(本题满分12分)
在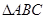 中,
中,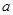 ,
,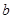 ,
,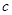 分别为内角
分别为内角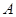 ,
,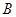 ,
,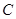 所对的边,且满足
所对的边,且满足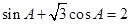 .
.
(Ⅰ)求角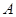 的大小;
的大小;
(Ⅱ)现给出三个条件:①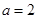 ;②
;②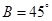 ;③
;③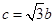 .
.
试从中选出两个可以确定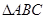 的条件,写出你的选择,并以此为依据求
的条件,写出你的选择,并以此为依据求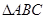 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
查看答案和解析>>
科目:高中数学 来源: 题型:
在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为内角
分别为内角![]() ,
,![]() ,
,![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)现给出三个条件:①![]() ;②
;②![]() ;③
;③![]() .
.
试从中选出两个可以确定![]() 的条件,写出你的选择,并以此为依据求
的条件,写出你的选择,并以此为依据求![]() 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com