练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数y = 1n|x－1|的图像与函数y="-2" cos 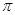x（-2≤x≤4）的图像所有交点的横坐标之和等于

    A．8                B．6                C．4                D．2

     

    【答案】

    B

    【解析】

    试题分析：在同一平面直角坐标系中，画出函数y = 1n|x－1|的图像与函数y="-2" cos x（-2≤x≤4）的图像，易知函数y = 1n|x－1|的图像与函数y="-2" cos x（-2≤x≤4）的图像都关于直线x=1对称，且在直线x=1的左右两侧各有3个交点，3个交点都分别关于直线x=1对称，所以所有交点的横坐标之和等于6.

    考点：对数函数的图像；三角函数的图像；图像的变换；函数的性质；中点坐标公式。

    点评：此题主要考查数形结合的数学思想。做此题的关键是正确、快速的画出函数y = 1n|x－1|与函数y="-2" cos x（-2≤x≤4）的图像。属于中档题。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数y=f（x）满足对任意x1、x2∈R都有f（x1+x2）=f（x1）f（x2），且f（1）=2．
    （Ⅰ）求f（2）、f（3）、f（4），猜测一个计算f（n）（n∈N*）的公式（不要求证明）；
    （Ⅱ）设an=
    		log2f(
    1
    n
    )
    (n=1，2，3，…)    ，
    （1）证明：a1+a2+a3＞2；
    （2）证明：a1+a2+a3+…+an＜2
    		n
    (n∈N*)    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnax-
    x-a
    x
    （a≠0）
    （Ⅰ）求此函数的单调区间及最值
    （Ⅱ）求证：对于任意正整数n均有1+
    1
    2
    +
    1
    3
    +    …+
    1
    n
    ≥
    1
    2
    ln
    (2e)2
    n!
    ，其中e为自然对数的底数；
    （Ⅲ）当a=1时，是否存在过点（1，-1）的直线与函数y=f（x）的图象相切？若存在，有多少条？若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•江西）若函数h（x）满足
    ①h（0）=1，h（1）=0；
    ②对任意a∈[0，1]，有h（h（a））=a；
    ③在（0，1）上单调递减．则称h（x）为补函数．已知函数h（x）=(
    1-xp
    1+λxp
    )
    1
    p
    （λ＞-1，p＞0）
    （1）判函数h（x）是否为补函数，并证明你的结论；
    （2）若存在m∈[0，1]，使得h（m）=m，若m是函数h（x）的中介元，记p=
    1
    n
    （n∈N+）时h（x）的中介元为xn，且Sn=
    n
    i=1
    xi    ，若对任意的n∈N+，都有Sn＜
    1
    2
    ，求λ的取值范围；
    （3）当λ=0，x∈（0，1）时，函数y=h（x）的图象总在直线y=1-x的上方，求P的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•吉安县模拟）已知函数y=f（x）对任意的实数x，y都有f（x+y）=f（x）•f（y）且f（1）≠0
    （1）记an=f(n)，(n∈N*)，Sn=
    n
    i=1
    ai，设bn=
    2Sn
    an
    +1且{bn}为等比数列，求a1的值    ；
    （2）在（1）的条件下，设Cn=
    1
    1+2an
    证明：
    （i）对任意的x＞0，Cn≥
    1
    1+x
    -
    1
    (1+x)2
    (2an-x)    n∈N*
    （ii） C1+C2+…+Cn＞
    n2
    n+1
    n∈N*．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列五个命题：其中正确的命题有
    ②③④
    ②③④
    （填序号）．
    ①函数y=sinx（x∈[-π，π]）的图象与x轴围成的图形的面积S=
    ∫
    π
    -π
    sinxdx    ；
    ②
    C
    r+1
    n+1
    =
    C
    r+1
    n
    +
    C
    r
    n
    ；
    ③在（a+b）n的展开式中，奇数项的二项式系数之和等于偶数项的二项式系数之和；
    ④i+i2+i3+…i2012=0；
    ⑤用数学归纳法证明不等式
    1
    n+1
    +
    1
    n+2
    +
    1
    n+3
    +…+
    1
    2n
    ＞
    13
    24
    ，(n≥2，n∈N*)    的过程中，由假设n=k成立推到n=k+1成立时，只需证明
    1
    k+1
    +
    1
    k+2
    +
    1
    k+3
    +…+
    1
    2k
    +
    1
    2k+1
    +
    1
    2(k+1)
    ＞
    13
    24
    即可．

    查看答案和解析>>

    同步练习册答案