解:(I)∵a
n+1=a
n+1,n∈N
*,∴a
n+1-a
n=1,n∈N
*…(2分)
∴数列{a
n}是以2为首项,1为公差的等差数列. …(4分)
∴a
n=n+1…(5分)
( II)∵a
n=n+1,
∴
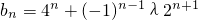
. …(6分)
∴要使b
n+1>b
n恒成立,
只要
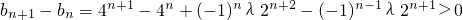
恒成立,
∴3•4
n-3λ•(-1)
n-12
n+1>0恒成立,
∴(-1)
n-1λ<2
n-1恒成立. …(8分)
(ⅰ)当n为奇数时,即λ<2
n-1恒成立,由于当且仅当n=1时,2
n-1有最小值为1,∴λ<1. …(10分)
(ⅱ)当n为偶数时,即λ>-2
n-1恒成立,当且仅当n=2时,-2
n-1有最大值-2,
∴λ>-2…(12分)
综上知-2<λ<1,再由λ为非零整数,可得λ=-1.
综上所述,存在λ=-1,使得对任意n∈N
*,都有b
n+1>b
n. …(13分)
分析:(I)由a
n+1=a
n+1,n∈N
*,可得数列{a
n}是以2为首项,1为公差的等差数列,从而求得数列{a
n}的通项公式.
(II)先求出{b
n}的通项公式,由条件可得(-1)
n-1λ<2
n-1恒成立,分n为奇数和n为偶数分别求出λ的取值范围,再由λ为非零整数,可得λ的值.
点评:本题主要考查数列的函数特性,函数的恒成立问题,等差数列的通项公式的应用,属于基础题.

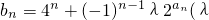 为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.
为非零整数,n∈N*),试确定λ的值,使得对任意n∈N*,都有bn+1>bn成立.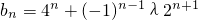 . …(6分)
. …(6分)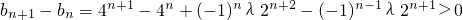 恒成立,
恒成立,

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案