Question

（06年江西卷理）（12分）

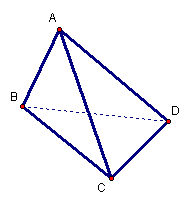
如图，在三棱锥A－BCD中，侧面ABD、ACD

是全等的直角三角形，AD是公共的斜边，

且AD＝，BD＝CD＝1，另一个侧面是正三角形

（1）求证：AD^BC

（2）求二面角B－AC－D的大小

（3）在直线AC上是否存在一点E，使ED与面BCD

成30°角？若存在，确定E的位置；若不存在，说明理由。

Answer 1

解析：解法一：

（1）方法一：作AH^面BCD于H，连DH。

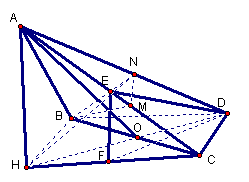
AB^BDÞHB^BD，又AD＝，BD＝1

\AB＝＝BC＝AC  \BD^DC

又BD＝CD，则BHCD是正方形，则DH^BC\AD^BC

方法二：取BC的中点O，连AO、DO

则有AO^BC，DO^BC，\BC^面AOD

\BC^AD

（2）作BM^AC于M，作MN^AC交AD于N，则ÐBMN就是二面角B－AC－D的平面角，因为AB＝AC＝BC＝\M是AC的中点，且MN¤¤CD，则BM＝，MN＝CD＝，BN＝AD＝，由余弦定理可求得cosÐBMN＝

\ÐBMN＝arccos

（3）设E是所求的点，作EF^CH于F，连FD。则EF¤¤AH，\EF^面BCD，ÐEDF就是ED与面BCD所成的角，则ÐEDF＝30°。设EF＝x，易得AH＝HC＝1，则CF＝x，FD＝，\tanÐEDF＝＝＝解得x＝，则CE＝x＝1

故线段AC上存在E点，且CE＝1时，ED与面BCD成30°角。

解法二：此题也可用空间向量求解，解答略